Mock test #1 ‘23: Full-syllabus test
Timings: 14:00-17:00 Hrs Date: 17 March 2023
Part A: Short-answer type questions
Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg or PartA.png.
For this part, answers must be written without any explanation.
For how many integers \(a\) with \(1 \leq a \leq 100\), is \(a^{a}\) a perfect square?
(a) 50
(b) 51
(c) 55
(d) 56Let \(A\) be a non-empty subset of real numbers and \(f: A \rightarrow A\) be a function such that \(f(f(x))=x\) for all \(x \in A\). Then \(f(x)\) is
(a) a bijection
(b) one-one but not onto
(c) onto but not one-one
(d) neither one-one nor ontoIf \(a+b+c=0\), then the quadratic equation \(3 a x^{2}+2 b x+c=0\) has
(a) at least one root in \((0,1)\)
(b) one root in \((1,2)\) and the other in \((-1,0)\)
(c) both imaginary roots
(d) a repeated rootThe system of equations \begin{gathered} 2 x+p y+6 z=8 \\ x+2 y+q z=5 \\ x+y+3 z=4 \end{gathered} has no solution for
(a) \(p \neq 2, q \neq 3\)
(b) \(p \neq 2, q=3\)
(c) \(p=2, q=3\)
(d) \(p=2, q \neq 3\)A relation \(R\) is defined on the set of positive integers as \(x R y\) if \(2 x+y \leq 5\). The relation \(R\) is
a) reflexive
b) symmetric
c) transitive
d) None of theseAn ant starts at the point \((0,0)\). It can travel along the integer lattice, only moving in the positive \(x\) and \(y\) directions. In how many ways it can reach \((4,4)\) without passing through \((2,2)\)? Write only the answer.
In the circle given below, the diameter \( \overline{EB} \) is parallel to \(\overline{DC}\) and \( \overline{AB} \) is parallel to \( \overline{ED} \). Also, \(\angle AEB\) and \(\angle ABE\) are in the ratio of 4:5. Which of the following statements are true?
(a) \(\angle ABE + \angle BCD = 180^\circ \)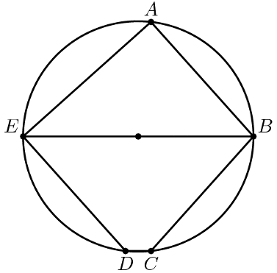
(b) \( \angle BCD = 120^\circ \)
(c) \( \angle BCD = 130^\circ \)
(d) \( \angle ABE = 40^\circ \)Suppose \(a\) and \(b\) are real numbers such that: \[ \lim_{x \rightarrow 0} \frac{\sin ^2 x}{e^{a x}-b x-1}=\frac{1}{2} \] What are the possible values for the ordered pair \( (a, b) \)?
(a) (2,2)
(b) (2,-2)
(c) (-2,2)
(d) (-2,-2)Let \(\operatorname{Im}(z)\) denote the imaginary part of the complex number \(z\). What is the value of the expression \( \operatorname{Im}\left(\sum_{n=0}^{\infty} \frac{e^{i n x}}{n !}\right) \)?
(a) \(e^{\cos x} \sin \sin x\)
(b) \(e^{\sin x} \sin \cos x\)
(c) \(e^{\cos x} \cos \sin x\)
(d) \(e^{\sin x} \cos \cos x\)Which of the following inequalities are true for any natural number \(n>4\)?
(a) \( \sqrt{n} \leq \sqrt[n]{n !} \)
(b) \( \sqrt[n]{n !} \leq \frac{n+1}{2}\)
(c) \( \sqrt{n} \geq \sqrt[n]{n !} \)
(d) \( \sqrt[n]{n !} \geq \frac{n+1}{2}\)
Part B: Subjective questions
Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.
Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.
B1. A pair of prime numbers that differ by 2 are called twin primes. Examples of twin primes are \( \{3,5\} \), \( \{11,13\} \), etc.
(a) Prove that every twin prime pair other than \( \{3,5\} \) must be of the form \( \{6k-1,6k+1\} \) where \(k\) is a positive integer. [2 marks]
(b) Prove that for any prime number \( p \geq 7\), the numbers \( p-2, p, p+2 \) cannot be in an arithmetic progression of primes. [2 marks]
(c) Find the number of primes \(p\) such that \(p, p+10, p+14\) are all prime numbers. [6 marks]
B2. Consider the \(n\)th degree polynomial \( p(x)=n\left(x^n+1\right)-2\left(x^{n-1}+\cdots+x\right) \). If \(n>1\), how many negative coefficients does \(p(x)^2\) have? Express your answer in terms of \(n\) and explain your reasoning.
B3. Let \( f\) be a function defined on natural numbers as follows. \( f(1) = 1 \) and for every \(n>1\), \(f\) is given by: \[ f(n) = f(n-\lfloor \sqrt{n} \rfloor) + n \] In the above relation \( \lfloor x \rfloor \) denotes the greatest integer less than or equal to \(x\). From the above equation we can derive the first few values of \( f\): \[ \begin{aligned} f(1) &= 1\\ f(2) &= f(2-\lfloor \sqrt{2} \rfloor ) + 2 = f(1) + 2 = 3\\ f(3) &= f(3-\lfloor \sqrt{3} \rfloor ) + 3 = f(2) + 3 = 6 \end{aligned} \] (a) Find the values of \( f(4) \) and \( f(5) \). [2 marks]
(b) Prove that there exists a positive number \(n_0\) such that \(f(n) \leq 3n\sqrt{n} \) for every \(n > n_0\). [8 marks]
B4. Ramesh and Kiran are two friends who practice piano every day at school. Ramesh goes to the piano room every day at a random time between 1 PM and 8 PM. He practices for three hours. Kiran goes to the piano room every day at a random time between 5 PM and 11 PM and practices for one hour. The block of time practice need not be contained in the given time interval for the arrival. For example, Ramesh could arrive at 7 PM and practice till 10 PM.
(i) What is the probability that Ramesh and Kiran meet on a given day? [7 marks]
(ii) What is the probability that Ramesh and Kiran meet on at least two days in a given span of 5 days? [3 marks]
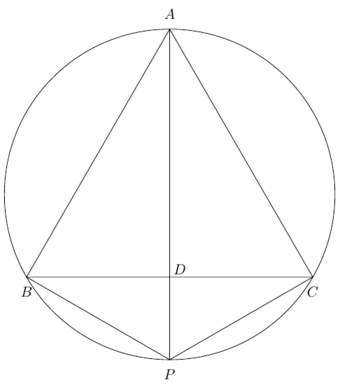
B5. In the figure given below, \(ABC\) is an equilateral triangle. The line drawn from vertex \(A\) meets \(BC\) at \(D\) and the circumcircle at \(P\). Prove that
(i) \(PA = PB + PC\)
(ii) \(\frac{1}{PD} = \frac{1}{PB} + \frac{1}{PC}\)
B6. Consider the function \( f(r) \):
\[ f(r)=\int_0^{\pi / 2} x^r \sin x d x \] Prove that:
(i) \( f(r) < \frac{(\pi / 2)^{r+1}}{r+1} \qquad \) [2 marks]
(ii) \( f(r) > \frac{(\pi / 2)^{r+1}}{r+2} \qquad \) [5 marks]
(iii) \( \int_0^{\pi / 2} x^r \cos x d x=\frac{f(r+1)}{r+1} \qquad \) [3 marks]