Integrals
A routine substitution
A4, 2018
Evaluate:
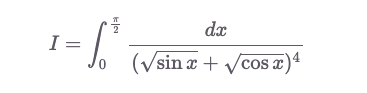
Solution
Multiply both the numerator and denominator by \(\sec^2 x\).
\begin{align} & I =\int_{0}^{\pi / 2} \frac{\mathrm{sec}^{2} x \mathrm{d} x}{(\sqrt{\tan x}+1)^{4}} \\\\ \mathrm{let} \tan x=t^{2} & \Rightarrow \sec^2 x \mathrm{d} x=2 t\mathrm{d}t \\\\ \Rightarrow \quad & I =\int_{0}^{\infty} \frac{2t \mathrm{d}t}{(t+1)^{4}} \Rightarrow I =\int_{0}^{\infty}\left[\frac{2}{(t+1)^{3}}-\frac{2}{(t+1)^{4}}\right] \mathrm{d}t \\ \Rightarrow \quad & I=\left.\frac{-1}{(\mathrm{t}+1)^{2}}+\frac{2}{3(\mathrm{t}+1)^{3}}\right\rvert_{0}^{\infty} \\ \Rightarrow \quad & I=\frac{1}{3} \end{align}
Problem credits

The Stanford Math Tournament (SMT) is an annual student-run math competition for high school students. It has been running since 1999. The above problem is taken from its 2013 calculus question paper (P9).
Absolute integrals
A7, 2017
Evaluate:
(a) \(\int_{-3}^{3}\left|3 x^{2}-3\right| d x\)
(b) \(f^{\prime}(1)\) where \(f(t)=\int_{0}^{t}\left|3 x^{2}-3\right| d x\)
Solution
(a) Due to symmetry, we can double the integral from 0 to 3. So the value is \(2I\), where:
\begin{align} I &=\int_{0}^{1} (3-3x^{2}) \text{d}x + \int_{1}^{3} (3 x^{2}-3) \text{d}x \\ &=\left. 3x-x^3 \right\rvert_{0}^1 + \left. (x^{3}-3x)\right\rvert_{1}^3 \\ &=2 + 20 \\ &=22\\ \end{align} Hence, \(\int_{-3}^{3}\left|3 x^{2}-3\right| d x = 44 \).
(b) \(\left|3 x^{2}-3\right|\) is a continuous function so by the fundamental theorem of calculus, \(f^{\prime}(1)=\) \(\left|3 \times 1^{2}-3\right|=0\)
Absolute integrals II
A3, 2020
(a) Evaluate \(\int_1^{e^2} \ln x dx\).
(b) Evaluate \(I = \int_{-1}^1 \frac{\ln\mid x\mid}{\mid x\mid}.\)
Solution
(a) \begin{align} \int_1^{e^2} \ln x \: \mbox{d}x &= x\ln x - x \rvert_{1}^{e^2} \\ &= [e^2\ln e^2 - e^2] -[ 1\ln 1 - 1] \\ &= e^2+1 \end{align}
(b) Since \(|x| = |-x|\), we have: \begin{align} \frac{I}{2} &= \int_{0}^1 \frac{\ln x}{x} \mbox{d}x \\ &= \left. \frac{(\ln x)^2}{2} \right \rvert_{0}^{1} \\ &= \frac{(\ln 1)^2}{2} - \frac{ (\ln 0)^2 }{2} \\ &=0-\infty \\ \therefore I &= -\infty \end{align}
Volume of a cave
B7, 2011
In this problem we want to find the volume of a cave described by equations. The base of the cave is in the XY-plane and the vertical direction is parallel to the Z-axis. The base of the cave lies in the XY-plane bounded by the parabola \(y^{2}=1-x\) and the Y-axis. Each cross-section of the cave perpendicular to the X-axis is a square.
(a) Show how to write a definite integral that will calculate the volume of this cave.
(b) Evaluate this definite integral. Can you find the volume without using indefinite integrals?
Solution
(a) The volume of the cave is given by the following triple integral:
\[ \int_{x=0}^{1} \int_{y=-\sqrt{1-x}}^{\sqrt{1-x}} \int_{z=0}^{2\sqrt{1-x}} \mathrm{d}x \mathrm{d}y \mathrm{d}z \] (b) \[ \int_{x=0}^{1} \int_{y=-\sqrt{1-x}}^{\sqrt{1-x}} 2\sqrt{1-x}\; \mathrm{d}x \mathrm{d}y \] \[ \int_{x=0}^{1} 4(1-x) \mathrm{d}x = 2 \text{m}^3 \]
Here is an alternate way to find the volume: The area of the cross-section of the cave goes from 4 sq.m to 0 sq.m linearly as \(x\) goes from 0 to 1. So volume is \(\frac{1}{2} \times 1 \times 4 = 2 \text{m}^3\).
Routine definite integral in disguise
B3, 2019
Evaluate \(\int_{0}^{\infty}\left(1+x^{2}\right)^{-(m+1)} d x,\) where \(m\) is a natural number.
Solution
Put \(x=\tan u\). This changes the integral to \[ I= \int_{0}^{\pi/2}\cos^{2m}(u) du \] \[ I=\frac{1}{4} \int_{0}^{2 \pi}\cos^{2m}(u) du \] \[\begin{aligned} \cos ^{n} \theta &=2^{-n}\left(\mathrm{e}^{\mathrm{i} \theta}+\mathrm{e}^{-\mathrm{i} \theta}\right)^{n} \\ &=2^{-n} \sum_{k=0}^{n}\left(\begin{array}{l}n \\ k\end{array}\right) \mathrm{e}^{\mathrm{i} k \theta} \mathrm{e}^{-\mathrm{i}(n-k) \theta} \\ &=2^{-n} \sum_{k=0}^{n}\left(\begin{array}{l}n \\ k\end{array}\right) \mathrm{e}^{\mathrm{i}(2 k-n) \theta} \\ \cos^{2m}\theta &=2^{-2m} \sum_{k=0}^{2m} \binom{2m}{k} \mathrm{e}^{\mathrm{i}(2k-2m) \theta \quad\quad\quad (1) } \end{aligned}\] \[\text{ Since } \int_{0}^{2 \pi} e^{i \ell x} d x=\left\{\begin{array}{ll}2 \pi & (\ell=0) \\ 0 & (\ell \neq 0)\end{array}\right.\] only one term in \((1)\) is non-zero, when \(k=m\). \[\int_{0}^{2 \pi} \cos ^{2m} x d x=\frac{2 \pi}{2^{2m}} \binom{2m}{m} \] \[I = \frac{1}{4} \cdot \frac{2\pi}{2^{2m}} \cdot \binom{2m}{m}\]
Convergence of \(e^{\text{quadratic}}\)
A2, 2014
Consider the integral \(I=\int_{1}^{\infty} e^{a x^{2}+b x+c} d x,\) where \(a, b, c\) are constants. Some combinations of values for these constants are given below and you have to decide in each case whether the integral \(I\) converges.
(A) \(I\) converges for \(a=-1 \quad b=10 \quad c=100\)
(B) \(I\) converges for \(a=1 \quad b=-10 \quad c=-100\)
(C) \(I\) converges for \(a=0 \quad b=-1 \quad c=100\)
(D) \(I\) converges for \(a=0 \quad b=0 \quad c=-100\)
Solution
TFTFA perplexing integral
B5, 2010
Prove that \(\int_{1}^{b} a^{\log_{b} x} d x>\ln b\) where \(a, b>0, b \neq 1\).
No solution
There is a mistake in this problem. The above statement is not true. See this discussion on Math Stack Exchange for details.
Riemann sum
B4, 2012
Define \[ x=\sum_{i=1}^{10} \frac{1}{10 \sqrt{3}} \frac{1}{1+\left(\frac{i}{10 \sqrt{3}}\right)^{2}} \] \[ y=\sum_{i=0}^{9} \frac{1}{10 \sqrt{3}} \frac{1}{1+\left(\frac{i}{10 \sqrt{3}}\right)^{2}} \]
Prove the two inequalities:
(a) \(x<\frac{\pi}{6}<y\)
(b) \(\frac{x+y}{2}<\frac{\pi}{6}\)
Hint: Connect the sums to an integral.
Solution (a)
a) Let \(f(t)=1 /\left(1+t^{2}\right) .\) Then \(y\) and \(x\) are respectively the left and right hand Riemann sums for \(f\) over the interval \(\left[0, \frac{1}{\sqrt{3}}\right]\) using 10 equal parts, each of width \(1 / 10 \sqrt{3} .\) since \(f\) is a positive decreasing function, \(y\) must be greater than the area under \(f\) over the given interval and \(x\) must be lesser than the area. The area under \(f\) over \(\left[0, \frac{1}{\sqrt{3}}\right]\) is:
\[\int_{0}^{1 / \sqrt{3}} f(t) d t=\lvert \tan^{-1}(t)\rvert_{0}^{1 / \sqrt{3}}=\frac{\pi}{6}\]
This implies that \(x< \frac{\pi}{6}< y\).
Solution (b)
b) \(\frac{x+y}{2}\) can be interpreted as the sum of areas of 10 trapezoids as follows. Dividing \(\left[0, \frac{1}{\sqrt{3}}\right]\) into 10 equal parts, let the \(i\)th subinterval be \(\left[x_{i}, x_{i+1}\right]\) with \(i=0,1, \ldots, 10 .\) Then the \(i\) -th trapezoid has base \(\left[x_{i}, x_{i+1}\right]\) and it has two vertical sides, the left one of height \(f\left(x_{i}\right)\) and the right one of height \(f\left(x_{i+1}\right)\).
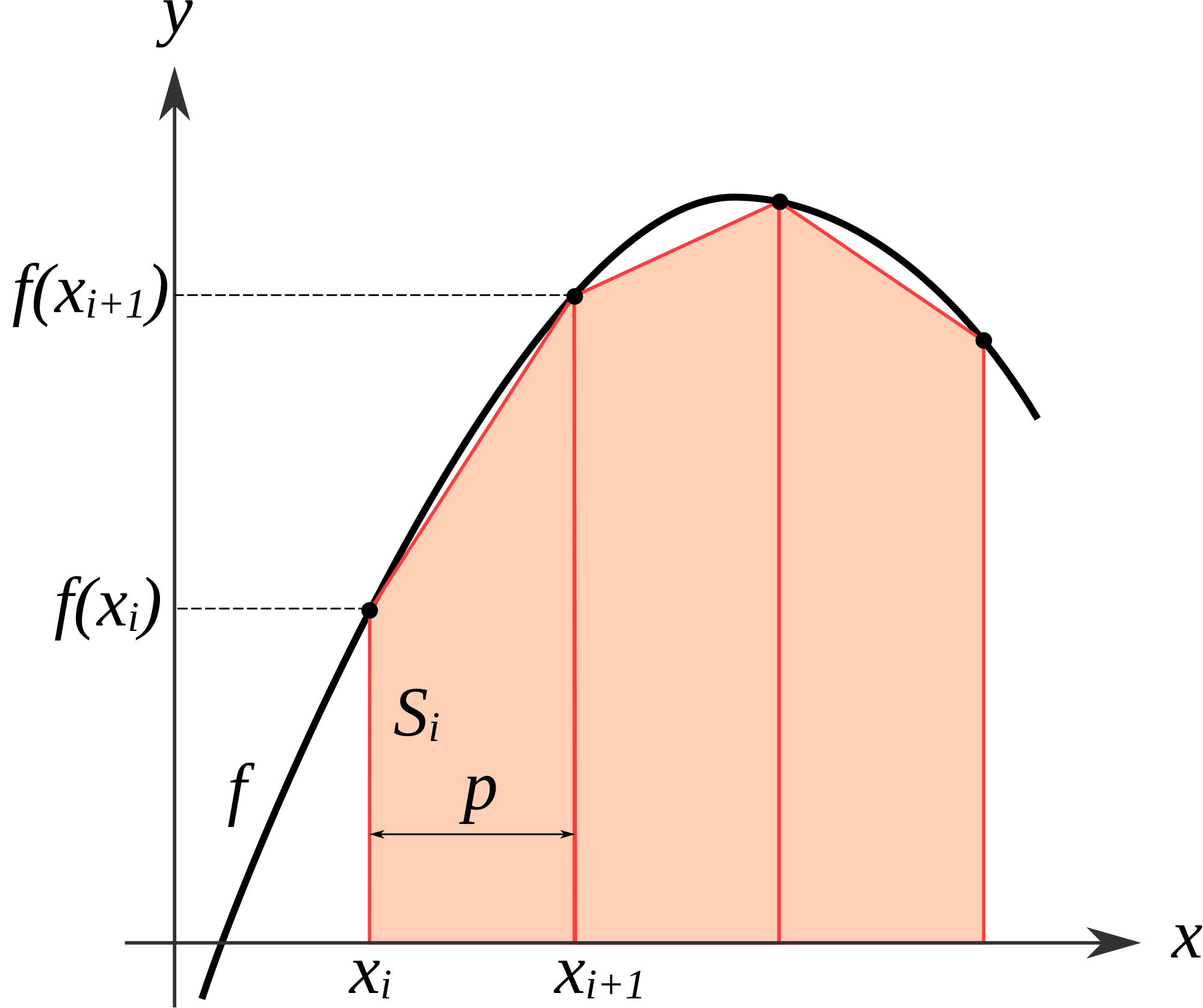
Claim: The function \(f\) is concave
Proof: In the interval \(\left(0, \frac{1}{\sqrt{3}}\right)\), we have \(f^{\prime \prime}(t)=\frac{6 t^{2}-2}{\left(1+t^{2}\right)^{3}}<0\). \(\square\).
Since \(f\) is concave, the total area of trapezoids is less than the area under \(f\).
Vanilla integrals
A6, 2013
Compute the integrals below, whenever possible. If it does not exist, say so.
The notation \([x]\) denotes the integer part of \(x\).
- (a) \(\int_{1}^{4} x^{2} d x\).
- (b) \(\int_{1}^{3}[x]^{2} d x\).
- (c) \(\int_{1}^{2}\left[x^{2}\right] d x\).
- (d) \(\int_{-1}^{1} \frac{1}{x^{2}} d x\).
Solution
a) \(\int_{1}^{4} x^{2} d x=\frac{x^{3}}{3}\rvert_{1} ^{4}=21\) using the fundamental theorem of calculus.
b) \(\int_{1}^{3}[x]^{2} d x=1\left(1^{2}\right)+1\left(2^{2}\right)=5=\) area under the piecewise constant function \([x]^{2}\)
c) \(\int_{1}^{2}\left[x^{2}\right] d x=1(\sqrt{2}-1)+2(\sqrt{3}-\sqrt{2})+3(2-\sqrt{3})=5-\sqrt{2}-\sqrt{3}\) since the function \([x]^{2}\) is constant on intervals \([1, \sqrt{2}),[\sqrt{2}, \sqrt{3}),[\sqrt{3}, 2)\). It takes the values 1,2 and 3 on these intervals, respectively.
d) \(\int_{-1}^{1} \frac{1}{x^{2}} d x=2 \lim_{t \rightarrow 0^{+}} \int_{t}^{1} \frac{1}{x^{2}} d x=2 \lim_{t \rightarrow 0^{+}}\left(-1+\frac{1}{t}\right)=\infty .\) The fundamental theorem does not apply over the interval [-1,1] because \(\frac{1}{x^{2}}\) goes to \(\infty\) in the interval. So the integral does not exist.
Differentiability Challenge
B4, 2014
(i) Let \(f\) be continuous on [-1,1] and differentiable at \(0 .\) For \(x \neq 0,\) define a function \(g\) by \(g(x)=\frac{f(x)-f(0)}{x} .\) Can \(g(0)\) be defined so that the extended function \(g\) is continuous at \(0 ?\)
(ii) For \(f\) as in part (i), show that the following limit exists.
\[ \lim_{r \rightarrow 0^{+}}\left(\int_{-1}^{-r} \frac{f(x)}{x} d x+\int_{r}^{1} \frac{f(x)}{x} d x\right) \]
(iii) Give an example showing that without the hypothesis of \(f\) being differentiable at \(0,\) the conclusion in (ii) need not hold.
Solution (i)
(i) Yes. We must define \(g(0)=\lim_{x \rightarrow 0} g(x)=f^{\prime}(0),\) which exists by hypothesis.
Solution (ii)
(ii) Consider \(\int_{-1}^{-r} g(x) d x=\int_{-1}^{-r} \frac{f(x)}{x} d x-\int_{-1}^{-r} \frac{f(0)}{x} d x=\int_{-1}^{-r} \frac{f(x)}{x} d x-f(0) \ln r . \quad\) Similarly
\[\int_{r}^{1} g(x) d x=\int_{r}^{1} \frac{f(x)}{x} d x-\int_{r}^{1} \frac{f(0)}{x} d x=\int_{r}^{1} \frac{f(x)}{x} d x+f(0) \ln r\]
Thus the expression inside the given limit is equal to \(\int_{-1}^{-r} g(x) d x+\int_{r}^{1} g(x) d x,\) as \(\pm f(0) \ln r\) cancels out.
Applying the fundamental theorem of calculus to the continuous function \(g,\) we get an anti-derivative \(G\) of \(g,\) where \(G\) is defined on [-1,1] by \(G(t)=\int_{-1}^{t} g(x) d x .\) So the given
\begin{align} \text { limit }&=\lim_{r \rightarrow 0^{+}}\left(\int_{-1}^{-r} g(x) d x+\int_{r}^{1} g(x) d x\right) \\ &=\lim_{r \rightarrow 0^{+}}(G(-r)-G(-1)+G(1)-G(r)) \\ &=G(0)-0+G(1)-G(0)\\ &=G(1) \end{align}
We have used the fundamental theorem to evaluate the integrals and the fact that \(G\) is differentiable.
Solution (iii)
(iii) Define \(f(x)=\frac{1}{-\ln \frac{x}{2}}\) for \(x \in(0,1], f(x)=\frac{1}{\ln \left|\frac{1}{2}\right|}\) for \(x \in[-1,0),\) and \(f(0)=0 .\) Verify that this works: \(f\) is continuous at 0 and so on \([-1,1] .\) It is not differentiable at 0 as the relevant limit is \(+\infty .\) The two integrals in the desired limit are equal (because \(f\) is an odd function, so \(\frac{f(x)}{x}\) is even \()\) and each integral is \(+\infty\) as it amounts to \(\lim_{t \rightarrow 0^{+}} \ln |\ln t| .\) Can you see how one might think of such \(f ?\) E.g., check that choices like \(|x|\) or even \(x^{\frac{1}{3}}\) do not work. Compare the behavior of these functions at \(x=0\) with that of chosen \(f .\)
Continuity based on integral conditions
A10, 2019
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\)
(a) There is no continuous function \(f\) for which \(\int_{0}^{1} f(x)(1-f(x)) d x<\frac{1}{4}\)
(b) There is only one continuous function \(f\) for which \(\int_{0}^{1} f(x)(1-f(x)) d x=\frac{1}{4}\)
(c) There are infinitely many continuous functions \(f\) for which \(\int_{0}^{1} f(x)(1-f(x)) d x=\frac{1}{4}\)
Solution
(a) False. \( f(x) = 0 \) is a counterexample.
(b) False. There are infinitely many candidates for \(f\). The maximum value of \( f(x)(1-f(x)) \) in the interval \(x \in (0,1)\) is \(1/4\). This value is attained only when \(f(x)=1/2\). So \(f\) is unique in the interval \( (0,1) \). But \(f\) is defined on \(\mathbb{R}\), so outside the interval \((0,1)\), it can be any continuous function.
(c) True. See part (b).
Slowly slope changing function
B4, 2015
Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a twice differentiable function, where \(\mathbb{R}\) denotes the set of real numbers. Suppose that for all real numbers \(x\) and \(y,\) the function \(f\) satisfies
\[ f^{\prime}(x)-f^{\prime}(y) \leq 3|x-y| \]
(a) Show that for all \(x\) and \(y,\) we must have \(\left|f(x)-f(y)-f^{\prime}(y)(x-y)\right| \leq 1.5(x-y)^{2}\)
(b) Find the largest and smallest possible values for \(f^{\prime \prime}(x)\) under the given conditions.
Solution
(a) Note that the given inequality stays valid if we take absolute value of the LHS, because we may interchange \(x\) and \(y\) without affecting RHS.
Fix \(x, y\) and let \(t=x-y .\) For now let \(x \geq y,\) i.e. \(t \geq 0 .\) For \(h \in[0, t],\) the value of \(y+h\) varies between \(y\) and \(x .\) We are given that \(\left|f^{\prime}(y+h)-f^{\prime}(y)\right| \leq 3|h|\). Integrate with respect to \(h\) over the interval \([0, t]\) to get: \[\int_{0}^{t}\left|f^{\prime}(y+h)-f^{\prime}(y)\right| d h \leq \int_{0}^{t} 3|h| d h=1.5 t^{2}\]
The following inequality follows from Lemma 1 (proved below).
\[\left|\int_{0}^{t} f^{\prime}(y+h)-f^{\prime}(y) d h\right| \leq \int_{0}^{t}\left|f^{\prime}(y+h)-f^{\prime}(y)\right| d h .\]
Combining with the previous inequality we have: \[\left|\int_{0}^{t} f^{\prime}(y+h)-f^{\prime}(y) d h\right| \leq 1.5 t^{2}\]
Finally we calculate the LHS.
\[\left|\int_{0}^{t} f^{\prime}(y+h) d h-\int_{0}^{t} f^{\prime}(y) d h\right|=\left|f(y+t)-f(y)-f^{\prime}(y) t\right|\]
where the first integral is calculated using the fundamental theorem of calculus and the second one is just the integral of the constant \(f^{\prime}(y) .\) Substituting \(x-y\) for \(t\) gives the desired result.
The case when \(x\leq y\) is analogous.
(b) We have, for \(x \neq y,\left|\frac{f^{\prime}(x)-f^{\prime}(y)}{x-y}\right| \leq 3,\) so \(-3 \leq \frac{f^{\prime}(x)-f^{\prime}(y)}{x-y} \leq 3 .\) Taking limit as \(y \rightarrow x\) we get \(-3 \leq f^{\prime \prime}(x) \leq 3 .\) It is easy to provide examples where \(f^{\prime \prime}\) attains the extreme values \(\pm 3,\) e.g. \(f(x)=\pm 1.5 x^{2} .\) These satisfy the hypothesis and have constant \(f^{\prime \prime}=\pm 3\)
Lemma 1.
\[ \left|\int_{a}^{b} f(x) d x\right| \leq \int_{a}^{b}|f(x)| d x \]
Proof.
\[ -|f(x)| \leq f(x) \leq|f(x)| \]
for all \(x\); hence
\[ -\int_{a}^{b}|f(x)| d x \leq \int_{a}^{b} f(x) d x \leq \int_{a}^{b}|f(x)| d x \]
The lemma follows since \(-a \leq x \leq a \implies |x|\leq a \) if \(a \geq 0\). \(\quad \square\)
Leibniz rule
B6, 2019
(a) Compute \(\frac{d}{dx}\left[\int_{0}^{e^{x}} \log (t) \cos ^{4}(t) dt\right]\)
(b) For \(x>0\) define \(F(x)=\int_{1}^{x} t \log (t) d t\)
i. Determine the open interval(s) (if any) where \(F(x)\) is decreasing and the open interval(s) (if any) where \(F(x)\) is increasing.
ii. Determine all the local minima of \(F(x)\) (if any) and the local maxima of \(F(x)\) (if any)
Solution
(a) The general form of Leibniz rule is:
\[\frac{\mathrm{d}}{\mathrm{d} x} \int_{a(x)}^{b(x)} f(x, t) \mathrm{d} t=f(x, b(x)) \cdot b^{\prime}(x)-f(x, a(x)) \cdot a^{\prime}(x)+\int_{a(x)}^{b(x)} \frac{\partial}{\partial x} f(x, t) \mathrm{d} t\]
Applying the rule above gives the following answer: \(e^{x} x \cos^{4}(e^{x})\)
(b)
\begin{aligned} F^{\prime}(x) &=\frac{d}{d x} \int_{1}^{x} t \log t \mathrm{d} t \\ &=x \log x \end{aligned}
Therefore \(F^{\prime}(1)=0 .\) Moreover, \(F^{\prime \prime}(x)=1+\log x .\) Hence one concludes that \(F\) is decreasing on \((0,1),\) increasing on \((1, \infty)\) and has a local minima at \(x=1\)
Sweep volume
A3, 2017
Find the volume of the solid obtained when the region bounded by \(y=\sqrt{x}, y=-x\) and the line \(x=4\) is revolved around the \(x\) -axis.
Solution
From \(x=0\) to \(x=1\) we have \(\sqrt{x} \geq|-x|,\) so from \(x=0\) to \(x=1\) the volume swept out by the curve determines the volume. From \(x=1\) to \(x=4\), the volume swept by the line determines the volume. Hence, we need two integrals.
From \(x=0\) and \(x=1\) we calculate volume obtained by revolving the area below \(y=\sqrt{x}\). \[ \int_{0}^{1} \pi (\sqrt{x})^2 \text{d}x = \left.\frac{\pi x^2}{2} \right\rvert_{0}^{1} = \frac{\pi\cdot 1^2}{2} - \frac{\pi\cdot 0^2}{2} = \frac{\pi}{2} \] Similarly, from \(x=1\) to \(x=4\) we have \(|-x| \geq \sqrt{x},\) so here we just have to take the volume obtained by the revolving the area below \(y=x\). \[ \int_{1}^{4} \pi x^2 \text{d}x = \left.\frac{\pi x^3}{3} \right\rvert_{1}^{4} = \frac{64\pi}{3} - \frac{\pi}{3} = 21\pi \] Thus total volume of the resulting solid: \( 21.5 \pi \).
Convergence of an improper integral
B5, 2021
Function \(f(x)\) is defined as \(f(0)=0\) and for \(x> 0\) as \[ f(x) = \lim_{L\rightarrow \infty} \int_{1/x}^{L} \frac{1}{t^2} \cos(t) dt \]
- Show that \(f(x)\) is well-defined.
- Find \(f'(1/\pi)\). Clearly state what result you are using.
- Find \( \lim_{h\rightarrow 0^+} \frac{f(h)-f(0)}{h} \).
Solution
- We split the function into three parts: \(A\) is the interval before the first time the function touches zero. \(B\) is the part of the function that is positive for \(x>\pi/2\) and \(C\) is the part of the function that is negative. We show that each of these intergrals converge.
\begin{align*} A:&\int_{1/x}^{\pi/2} \frac{\cos t}{t^2} dt\\ B:& \sum_{k=0}^{n} \int_{(2k+1)\pi/2}^{(2k+3)\pi/2} \frac{\cos t}{t^2} dt\\ C:& \sum_{k=0}^{n} \int_{(2k+3)\pi/2}^{(2k+5)\pi/2} \frac{\cos t}{t^2} dt\\ \end{align*} \(A\) is a proper integral and hence well-defined for a given \(x\). \(B\) and \(C\) are dominated by the integrals \( \int_{\pi/2}^{\infty} \frac{1}{t^2}\) and \( -\int_{\pi/2}^{\infty} \frac{1}{t^2} dt \), respectively and hence they converge.
- The general form of Leibniz rule is:
\[\frac{\mathrm{d}}{\mathrm{d} x} \int_{a(x)}^{b(x)} f(x, t) \mathrm{d} t=f(x, b(x)) \cdot b^{\prime}(x)-f(x, a(x)) \cdot a^{\prime}(x)+\int_{a(x)}^{b(x)} \frac{\partial}{\partial x} f(x, t) \mathrm{d} t\] Substituting, \( a(x) = 1/x \) and \(b(x)=L\), we get:
\begin{align*} f^\prime(x) &= 0- \frac{\cos(1/x)}{1/x^2}\cdot (-1/x^2) \\ f^\prime(1/\pi) &= \cos\pi = -1 \\ \end{align*} - Solution due to Soham Ghosh (West Bengal).
\begin{align*} f(x) &=\int_{1 / x}^{\infty} \frac{1}{t^{2}} \cos t \,dt \\ &=\left.\frac{1}{t^{2}} \sin t\right|_{1 / x} ^{\infty}-\int_{1 / x}^{\infty} \frac{(-2)}{t^{3}} \sin t\, dt \;\;\text{ (using integration by parts)} \\ &=-x^{2} \sin \frac{1}{x}+\int_{1 / x}^{\infty} \frac{2}{t^{3}} \sin t\, dt \\ \end{align*} We are required to calculate only the right-hand side limit. L'Hospital's rule is not applicable. \[ \lim_{h \rightarrow 0^{+}} \frac{f(h)-f(0)}{h}=\lim_{h \rightarrow 0^{+}} \frac{f(h)}{h} \] \begin{align*} f(h)&=-h^{2} \sin \frac{1}{h}+\int_{1 / h}^{\infty} \frac{2}{t^{3}} \sin t\, d t \\ \frac{f(h)}{h}&=-h \sin \frac{1}{h}+\frac{1}{h}\int_{1 / h}^{\infty} \frac{2}{t^{3}} \sin t\, d t \end{align*} We will show that the limit of each summand in the LHS goes to zero.
Firstly, \( \lim_{h\rightarrow 0} -h \sin \frac{1}{h} = 0 \).
\begin{align*} -\frac{2}{t^{3}} & \leq \frac{2}{t^{3}} \sin t \leq \frac{2}{t^{3}} \quad (\because-1 \leqslant \sin t \leqslant 1) \\ -\int_{1 / x}^{\infty} \frac{2}{t^{3}} d t &\leq \int_{1 / x}^{\infty} \frac{2}{t^{3}} \sin t\, dt \leq \int_{1 / x}^{\infty} \frac{2}{t^{3}} d t \\ -\left.2 \frac{t^{-2}}{-2}\right|_{1 / x} ^{\infty} &\leq \int_{1 / x}^{\infty} \frac{2}{t^{3}} \sin t\, dt \leq \left. 2 \frac{t^{-2}}{-2}\right|_{1 / x} ^{\infty} \\ -x^{2} &\leq \int_{1 / x}^{\infty} \frac{2}{t^{3}} \sin t\, d t \leq x^{2} \\ -h^{2} &\leq \int_{1 / h}^{\infty} \frac{2}{t^{3}} \sin t\, d t \leq h^{2} \\ -h &\leq \frac{1}{h} \int_{1 / h}^{\infty} \frac{2}{t^{3}} \sin t\, d t \leq h \\ \lim_{h\rightarrow 0^+}& \frac{1}{h} \int_{1 / h}^{\infty} \frac{2}{t^{3}} \sin t\, d t = 0 \;\; \text{ Hence proved.} \end{align*}
Definite integral
B3, 2016
Consider the function \(f(x)=x^{\cos (x)+\sin (x)}\) defined for \(x \geq 0\).
(a) Prove that
\[ 0.4 \leq \int_{0}^{1} f(x) d x \leq 0.5 \]
(b) Suppose the graph of \(f(x)\) is being traced on a computer screen with the uniform speed of \(1 \mathrm{cm}\) per second (i.e., this is how fast the length of the curve is increasing). Show that at the moment the point corresponding to \(x=1\) is being drawn, the \(x\) coordinate is increasing at the rate of
\[ \frac{1}{\sqrt{2+\sin (2)}} \mathrm{cm} \text { per second } \]
Solution
(a) It is easy to see that for \(0 \leq x \leq 1,\) we have \(1 \leq \cos (x)+\sin (x) \leq \sqrt{2},\) and so
\[ x^{1} \geq x^{\cos (x)+\sin (x)} \geq x^{\sqrt{2}} \]
As all three functions are non-negative in \([0,1],\) we can integrate the inequalities over that interval to get
\[ \frac{1}{2} \geq \int_{0}^{1} f(x) d x \geq \frac{1}{\sqrt{2}+1}>\frac{1}{1.5+1}=0.4 \]
(b) Length of the curve from \(x=0\) to any given \(x\) is \(l(x)=\int_{0}^{x} \sqrt{1+f^{\prime}(u)^{2}} d u\) It is given that \(\frac{d l}{d t}=1 \mathrm{cm} /\) second at all times. One needs to find \(\frac{d x}{d t}\) when \(x=1\)
By chain rule \( \displaystyle \frac{d l}{d t}=\frac{d l}{d x} \frac{d x}{d t} .\)
By the fundamental theorem of calculus:
\[\frac{d l}{d x}=\sqrt{1+f^{\prime}(x)^{2}}\]
From Lemma 1, we have \(f^{\prime}(1)=\cos (1)+\sin (1)\).
So at \(x=1\) we have
\[ \frac{d l}{d x}=\sqrt{1+(\cos (1)+\sin (1))^{2}}=\sqrt{2+\sin 2}\] The statement follows by substituting in the first equation.
Lemma 1: \(f^{\prime}(1) = \sin(1) + \cos(1)\)
\[f^{\prime}(x) = x^{(\cos (x)+\sin (x))-1}(-x \log (x) \sin (x)+x \log (x) \cos (x)+(\cos (x)+\sin (x))) \]
Substitute \(x=1\) and \(\log (1) = 0\) in the above equation.\(\;\square\)
