MT #12: Full-syllabus
Timings: 14:00-17:00 Hrs Date: 23 July 2021
Instructions
- You are responsible for keeping time. Email all your solutions by 17:05 Hrs IST.
- Write your answers with a dark pen on white paper.
- Find an email from me with the subject line ‘Mock test 12: Full-syllabus’. Send your solutions (images) as replies to this email.
- Adjust/Reduce the resolution of the camera so that each image is less than 500 KB in size.
- Total marks: 100 (10x4=40 for Part A + 6x10=60 for Part B)
For students who miss the live test (members only)
Self-administer the mock test and email your solutions before 24 July, 23:59 Hrs. Your solutions will be evaluated but marks won’t be counted for official use in the future. Solutions submitted after 24 July, 23:59 Hrs will not be evaluated. As per the rules of CMI entrance exam, no calculators or log tables must be used.
Part A: Short-answer type questions
Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg or PartA.png.
For this part, answers must be written without any explanation.
Find a value \(k\) such that \(f(x)=x^{2}+kx-17, f(4)=f^{\prime}(4)\).
Suppose we have a number \(x\) such that: \begin{align*} x & \equiv 1 \pmod{2}\\ x & \equiv 2 \pmod{3}\\ x & \equiv 3 \pmod{5} \end{align*} List all the possible values of \(x \pmod{30}\).
\(AEBCD\) is a pentagon such that \(ABCD\) is a rectangle and \(AEB\) is an isosceles triangle. A circle passes through \(A,B,C,D\) and \(E\). This circle has radius 1 unit. Find the value of \(|AD|\) for which the rectangle and triangle have the same area.
If \(a=(\sqrt{3}+\sqrt{2})^{-3}\) and \(b=(\sqrt{3}-\sqrt{2})^{-3}\). Find the value of: \[\frac{1}{(a+1)}+\frac{1}{(b+1)}\].
Find the value of \(n\) that maximizes\(\left|\sqrt{n^{2}+4 n+5}-\sqrt{n^{2}+2 n+5}\right|\).
Numbers from 1 to 9999 are written on a paper. How many times is the digit 2 written?
Suppose \(f: \mathbb{R} \rightarrow \mathbb{R}\) is an odd and differentiable function. Then for every \(x_{0} \in \mathbb{R}, f^{\prime}\left(-x_{0}\right)\) is equal to:
(a) \(f^{\prime}\left(x_{0}\right)\)
(b) \(-f^{\prime}\left(x_{0}\right)\)
(c) 0
(d) -1
(e) None of these.- How many ways are there to choose positive integers \(x\) and \(y\) such that the least common multiple of \(x\) and \(y\) is 144 ?
- Consider tangent circles \(\gamma_{1}\) and \(\gamma_{2}\) with centers \(O_{1}, O_{2}\) and radii \(R, r\) with \(r < R \), respectively. Let \(\overline{A B}\) be a common external tangent of length 16. The area of \(A B O_{1} O_{2}\) is 160. Find the ordered pair \((r, R)\).
Let \(a, b \in \mathbb{C}\) such that \(a+b=a^{2}+b^{2}=\frac{2 \sqrt{3}}{3} i\). Compute \(|\operatorname{Re}(a)|\).
Part B: Subjective questions
Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.
Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.
B1. Consider the quadratic function \(f(x)=x^{2}+b x+c\) defined on the set of real numbers. Given that the roots of \(f\) are two distinct prime numbers \(p\) and \(q\), and \(f(p-q)=6 p q\), determine the primes \(p\) and \(q\), and the function \(f\).
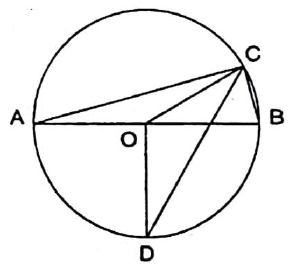
B2. \(AB\) is a diameter of a circle of radius \(10\) units. \(C\) is a point on the circle such that the length of arc \(B C=\frac{5 \pi}{3}\). The bisector of \(\angle A C B\) cuts the circle at \(D\). Find the length of \(CD\).
B3. Determine the number of positive integers \(n\) less than \(10000\) for which the sum \[ \frac{1}{2 \times\lfloor\sqrt{1}\rfloor+1}+\frac{1}{2 \times\lfloor\sqrt{2}\rfloor+1}+\frac{1}{2 \times\lfloor\sqrt{3}\rfloor+1}+\cdots+\frac{1}{2 \times\lfloor\sqrt{n}\rfloor+1} \] is an integer.
Notation. \(\lfloor x\rfloor\) denotes the largest integer that is less than or equal to \(x\).
B4. We say that a function \(f: \mathbb{R} \rightarrow \mathbb{R}\) is flippy if \(f(f(x))=-x\) for all \(x \in \mathbb{R}\)
(a) Prove or disprove: \(f\) is always injective.\(\;\;\;\) [2 marks]
(b) Give an example of a flippy function.\(\;\;\;\) [3 marks]
(c) Prove that there is no flippy function that is continuous. \(\;\;\;\) [5 marks]
B5. (a) Suppose \(p\) and \(q\) are relatively prime numbers. Compute the limit: \[ \lim_{k\rightarrow \infty} \sqrt{k^{2} q^{2}+2 p k}-\sqrt{k^{2} q^{2}} \;\;\;\;\;\text{[4 marks]}\]
(b) Find the value of: \(\displaystyle\lim_{x\rightarrow\infty}\dfrac{1}{x} \int_{0}^{x} \frac{1}{3+\cos t}dt\;\;\;\;\; \text{[6 marks]}\)
B6. A nonnegative integer \(k\) is special when all pairs of 1s in the binary representation of \(k\) are separated by at least two zeroes. For example, \(9=1001_{2}\) is special, but \(10=1010_{2}\) is not special. How many special numbers are less than \(2^{15}\)?