MT #11: Full-syllabus
Timings: 14:00-17:00 Hrs Date: 9 July 2021
Instructions
- You are responsible for keeping time. Email all your solutions by 17:05 Hrs IST.
- Write your answers with a dark pen on white paper.
- Find an email from me with the subject line ‘Mock test 11: Full-syllabus’. Send your solutions (images) as replies to this email.
- Adjust/Reduce the resolution of the camera so that each image is less than 500 KB in size.
- Total marks: 100 (10x4=40 for Part A + 6x10=60 for Part B)
- As per the rules of CMI entrance exam, no calculators or log tables must be used.
For students who miss the live test (members only)
Self-administer the mock test and email your solutions before 10 July, 23:59 Hrs. Your solutions will be evaluated but marks won’t be counted for official use in the future. Solutions submitted after 10 July, 23:59 Hrs will not be evaluated.
Part A: Short-answer type questions
Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg or PartA.png.
For this part, answers must be written without any explanation.
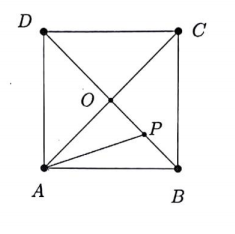
- \(ABCD\) is a unit square and \(P\) is the midpoint of segment \(OB\) in the figure below. What is the length of \(AP\)?
- Suppose \(2 \log x+\log y=x-y\). Then the equation of the tangent line to the graph of this equation at the point \((1,1)\) is:
(a) \(x+2 y=3\)
(b) \(x-2 y=3\)
(c) \(2 x+y=3\)
(d) \(2 x-y=3\) How many triples \(({A}, {B}, {C})\) are there of sets with union \({A} \cup {B} \cup {C}=\{1,2,3,4,5,6,7,8\}\) and \({A} \cap {B} \cap {C}=\varnothing ?\)
- Find all integers \(x\) for which \( |x^3+2x| \) is prime.
Given that \(a_{1}=2, a_{2}=3, a_{n}=a_{n-1}+2 a_{n-2}\), what is \(a_{19}+a_{20}\)?
A spirograph is a toy that has a cog and a rack. The cog and the rack have teeth that fit together. In the figure shown below, the cog has 12 teeth and the rack has 30.
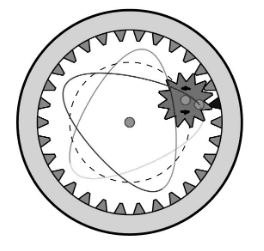
The cog has a hole near its circumference. If we put a pen in the hole and turn the cog around the rack many times, we get a pattern. In the example shown above, we get a pattern with five pointed ends. Pointed ends are those points in the pattern where the pen is closest to the rack.
Suppose the cog had 9 teeth and the rack had 20. How may pointed ends would the pattern have?
- \[ \lim_{x \rightarrow 0}\left(\frac{\sin x}{x}\right)^{\frac{1}{1-\cos x}} \]
- How many positive integers divide at least one of \(10^{30}\) and \(20^{30}\) ?
Suppose that the set \(\{1,2, \cdots, 2022\}\) has been partitioned into disjoint pairs \(\left\{a_{i}, b_{i}\right\}(1 \leq i \leq 1011)\) so that for all \(i,\left|a_{i}-b_{i}\right|\) equals 1 or 6. Find all the possible values for the last digit of the sum: \[ \left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|+\cdots+\left|a_{1011}-b_{1011}\right| \]
There is a highway on which a group of police officers are testing for drunk-driving. They have breathalyzers that raises a false alarm in 5% of the cases in which the driver is sober. That is, even if the driver is not drunk there is a 5% chance that the breathalyzer incorrectly shows him to be drunk. However, the breathalyzer never fails to detect a truly drunk person. We know for a fact that one in a every thousand drivers on the highway is driving drunk. Suppose the police officers stop a driver at random to administer a breathalyzer test. It indicates that the driver is drunk. The probability that he is truly drunk is around:
(a) 2%
(b) 10%
(c) 20%
(d) 95%
Part B: Subjective questions
Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.
Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.
B1. Prove or disprove: There are two numbers \(x, y\) such that: \begin{align*} x+y&=1\\ x^{2}+y^{2}&=2\\ x^{3}+y^{3}&=3 \end{align*}
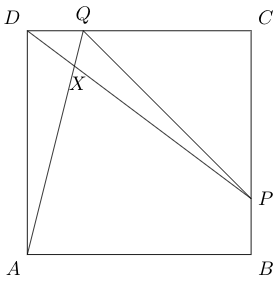
B2. In the figure shown below, \(ABCD\) is a square with side length of \(4\) cm. \(DQ=BP=1\) cm. Line segments \(AQ\) and \(DP\) intersect at point \(X\). Find the area of the triangle \(PQX\).
B3. (a) Suppose we have a polynomial \(p(x) = a_n x^n + a_{n-1}x^{n-1} + \cdots + a_0\) where \(a_i\)s are real numbers. If \( \sum \frac{a_i}{i+1} = 0 \), prove that \(p(x)\) has a real root between 0 and 1. \(\;\;\;\) [4 marks]
(b) Evaluate the following integral: \[ \int_{0}^{\pi} \frac{x \sin x}{1+\cos ^{2} x} d x \;\;\;\;\;\;\;\; \text{[6 marks]} \]
B4. Determine all polynomials \(f(x)=a x^{2}+b x+c\) such that \(f(a)=a, f(b)=b\) and \(f(c)=c\).
B5. A special matrix is a square matrix whose entries are \(0\) or \(1\) such that, in each row, the \(1\)s appear as consecutive entries. For example, the following is a \(4 \times 4\) special matrix. \[ \left[\begin{array}{llll} 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 \end{array}\right] \] Show that the determinant of any special matrix is either \(1,-1\) or \(0\).
B6. Show that the number \(4^{2020}\) cannot be written as a sum of three cubes. In other words, prove that there are no integers \(a_1,a_2\) and \(a_3\) such that \[ a_1^3 + a_2^3 + a_3^3 = 4^{2020} \]