Link Search Menu Expand Document
CMI Entrance Exam

MT #9: Full-syllabus

Timings: 14:00-17:00 Hrs    Date: 4 June 2021

Part A: Short-answer type questions

Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg.

For this part, answers must be written without any explanation.

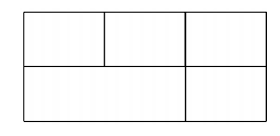
  1. Let \(n\) be a positive integer. Line segments can be drawn parallel to edges of a given rectangle. What is the minimum number of line segments that are required so as to divide the rectangle into exactly \(n\) subrectangles? The subrectangles need not be of the same dimension.

    For example, in order to get 5 subrectangles we need 3 line segments.

  2. The polynomial \( f(x)=a x^{2018}+b x^{2017}+c x^{2016} \) has real coefficients less than 2020 and \[ f\left(\frac{1+\sqrt{3} i}{2}\right)=2015+2019 \sqrt{3} i \] Write the value of \(f(1)\).

  3. Let \(X\) be a set and \(A, B, C\) be its subsets. Which of the following is necessarily true?
    (a) \(A-(A-B)=B\)
    (b) \(A-(B \cup C)=(A-B) \cup(A-C)\)
    (c) \(A-(B \cap C)=(A-B) \cap(A-C)\)
    (d) \(B-(A-B)=B\)

  4. Find the number of functions \(f:\{1,\ldots, 5\} \to \{1,\ldots, 5\}\) such that \(f(f(x))=x\) .

  5. The number of roots of \(g(x)=5 x^{4}-4 x+1=0\) in \([0,1]\) is
    (a) 0
    (b) 1
    (c) 2
    (d) 3

  6. Evaluate : \(\lim\limits_{n\to\infty} \displaystyle\int_{0}^{1} \left(1 + \frac{x}{n}\right)^n dx\)

  7. Consider a square \(ABCD\), whose length of a side is \(7\) units. Now, draw an equilateral triangle \(ABM\) so that the vertex \(M\) lies inside the square. The diagonal \(AC\) meets the triangle at the point \(K\). Find out the value of \(| CK - KM |\) .

  8. \(2021\) players numbered \(1, 2, \cdots , 2021\) took part in a table tennis tournament. Each player played exactly one game against each of the \(2020\) other players, and no match ended in a draw. Let \(W_k\) and \(L_k\) denote the number of matches won and lost respectively by the \(k\)-th player, for \(k = 1, 2, \cdots , 2021\). Find out which among the following options is correct :
    1. \(~~~~\displaystyle\sum_{k=1}^{2021} W^2_k = (2020)^2 - \displaystyle\sum_{k=1}^{2021} L^2_k\)
    2. \(~~~~\displaystyle\sum_{k=1}^{2021} W^2_k = \binom{2021}{2} + \displaystyle\sum_{k=1}^{2021} L^2_k\)
    3. \(~~~~\displaystyle\sum_{k=1}^{2021} W^2_k = (2020)^2 + \displaystyle\sum_{k=1}^{2021} L^2_k\)
    4. \(~~~~\displaystyle\sum_{k=1}^{2021} W^2_k = \displaystyle\sum_{k=1}^{2021} L^2_k\)
    5. \(~~~~\displaystyle\sum_{k=1}^{2021} W^2_k = 2021 + \displaystyle\sum_{k=1}^{2021} L^2_k\)

  9. Let \(\Lambda\) be the set of all \(n \in \mathbb{N}\) such that both the numbers \((n+3)\), and \((n^2 + 3n +3)\) are perfect cubes. Find the cardinality of the set \(\Lambda\).

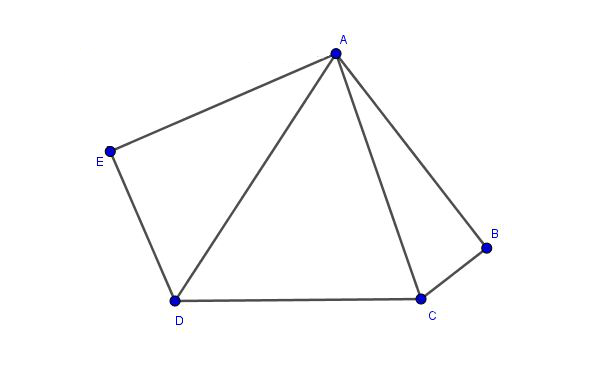
  10. Consider \(ABCDE\) to be a convex pentagon such that \(AB = AE = CD = 1\), \(\angle ABC = \angle DEA = 90^\circ\) , and \(BC + DE = 1\). Find the area of the pentagon.

Part B: Subjective questions

Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1. Find all real \(x\) for which the equation holds: \[ 4^{x}+9^{x}+36^{x}+\sqrt{\frac{1}{2}-2 x^{2}}=1 \]

B2. Consider a set of \(n\) islands \(X_1, \ldots , X_n\) arranged in a circle. Assume \(n\geq 2\). There are two bridges between each pair of neighboring islands. For example, the situation for \(n=5\) is shown below:

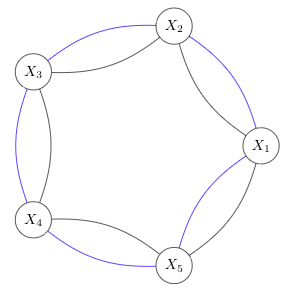
(a) Suppose we start from island \(X_1\) and cross the \(2n\) bridges exactly once. Show that we will return to \(X_1\) at the end of the journey. \(\;\;\) [2 marks]
(b) Stating from the island \(X_1\), how many ways one can cross the \(2n\) bridges so that each bridge is crossed exactly once? \(\;\;\) [8 marks]

B3. Consider the sequence of natural numbers \(a_1,a_2,\ldots,a_n\) defined as follows:

  • \(a_1=2\).
  • For each positive number \(n\), \(a_{n+1} = a_n + \) product of the prime factors of \(a_n\).
The first eight numbers of the sequence are: \( 2, 4, 6, 12, 18, 24, 30 \text{ and } 60 \).
(a) Does the number 210 appear in the sequence? \(\;\;\) [1 mark]
(b) Prove that the product of the first 2021 primes appears in the sequence. \(\;\;\) [9 marks]

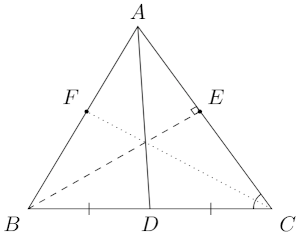
B4. \(A B C\) is an acute triangle with \(B C=4\) and \(A C=5\). Let \(D\) be the midpoint of \(BC\). \(BE\) is the altitude to \(AC\). \(CF\) is the angle bisector of \(\angle B C A\). If \(A D, B E\), and \(C F\) meet at a single point, compute the length of \(BE\).

B5. Consider a real polynomial of the form \(p(x) = ax^4 + bx^2+c \). We are given that \(0\leq p(x)\leq 1\) for all \(0 \leq x \leq 1\).

  1. Show that the above condition implies that \(a\leq 4\). \(\;\;\) [7 marks]
  2. Find a real polynomial with \(a=4\) that satisfies the given condition. \(\;\;\) [3 marks]

B6. Let \(\{a_k\}_{k \in \mathbb{N} }\) be a strictly increasing sequence of positive integers. Define the sequence \(\{s_n\}_{n \in \mathbb{N}}\) as \[ s_n=\sum_{k=1}^{n}\frac{1}{[a_k,a_{k+1}]}\] where \([a_k,a_{k+1}]\) is the least common multiple (i.e. LCM) of \(a_k\) and \(a_{k+1}\).

  1. Show that the sequence \(\{s_n\}_{n \in \mathbb{N}}\) is bounded above. \(\;\;\)[8 marks]
  2. Prove that \(\{s_n\}_{n \in \mathbb{N}}\) converges.\(\;\;\)[2 marks]