Link Search Menu Expand Document
CMI Entrance Exam

MT #8: Full-syllabus

Timings: 17:00-20:00 Hrs    Date: 20 May 2021

Instructions

  • You are responsible for keeping time. Email all your solutions by 20:05 Hrs IST.
  • Write your answers with a dark pen on white paper.
  • Find an email from me with the subject line ‘Mock test #8: Full-syllabus’. Send your solutions (images) as replies to this email.
  • Adjust/Reduce the resolution of the camera so that each image is less than 500 KB in size.
  • Total marks: 100 (10x4=40 for Part A + 6x10=60 for Part B)

For students who miss the live test (members only)
Self-administer the mock test and email your solutions before 21 May, 23:59 Hrs. Your solutions will be evaluated but marks won’t be counted for official use in the future. Solutions submitted after 21 May, 23:59 Hrs will not be evaluated. As per the rules of CMI entrance exam, no calculators or log tables must be used.

Part A: Short-answer type questions

Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg.

For this part, answers must be written without any explanation.

  1. Find all possible triplets \( (x,y,z) \) satisfying the equations: \begin{align*} (x+1)(y+1)&=24 \\ (y+1)(z+1)&=8 \\ (z+1)(x+1)&=48 \end{align*}

  2. There is a glass cylinder with radius \(R\). An ant is \(d\) cm from the mouth of the cylinder. It is on the outer surface of the cylinder. There is a honey drop on the inner surface of cylinder that is also \(d\) cm from the mouth of the cylinder and diametrically opposite to the ant. What is the shortest distance the ant has to travel to get to the honey drop?

  3. In the triangle \(ABC\) given below, \(BC=8\) cm and \(AD=6\) cm. \(AD\) is the altitude of the triangle. Points \(E\) and \(G\) are midpoints of segments \(BD\) and \(AC\), respectively. What is the length of \(EG\)?

  4. Let \(A\) be a non-empty subset of real numbers and \(f: A \rightarrow A\) be a function such that \(f(f(x))=x\) for all \(x \in A\). Then \(f(x)\) is
    1. a bijection.
    2. one-one but not onto.
    3. onto but not one-one.
    4. neither one-one nor onto.
    5. Not confined exclusively to one of the above four options.

  5. Which of the following functions are bijections?
    1. \(f: \mathbb{R} \rightarrow \mathbb{R} \) defined as \( f(x):=x+\tan^{-1}x \).
    2. \(f: \mathbb{R} \rightarrow \mathbb{R} \) defined as \( f(x):=x-\tan^{-1}x \).
    3. \(f:\, \mathbb{R}^+ \rightarrow \mathbb{R} \) defined as \( f(x):=\lim_{n\rightarrow \infty} \frac{1}{n} \log_{e} (1+e^{nx}) \).

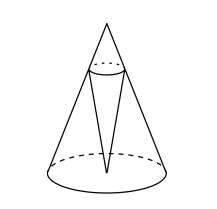
  6. A cone with height \(h\) is inscribed in a larger cone with height \(H\). The vertex of the inner cone is at the center of the base of the larger cone. For what value of \(h\) is the volume of the inner cone maximized?

  7. An ATM machine dispenses one note at a time. We can collect either a Rs. 100, Rs. 200 or Rs. 500 note in one operation. We can collect a certain sum in multiple ways. For example, there are three different ways to collect a sum of Rs. 300: 100+200, 200+100 or 100+100+100. What is the minimum sum that we can collect in at least 30 different ways?

  8. Let \(f\) be a twice differentiable function on \(\mathbb{R}\). Also \(f^{\prime \prime}(x)>0\) for all \(x \in \mathbb{R}\). Which of the following statements is true?
    1. \(f(x)=0\) has exactly two solutions on \(\mathbb{R}\).
    2. \(f(x)=0\) has a positive solution if \(f(0)=0\) and \(f^{\prime}(0)=0\).
    3. \(f(x)=0\) has no positive solution if \(f(0)=0\) and \(f^{\prime}(0)>0\).
    4. \(f(x)=0\) has no positive solution if \(f(0)=0\) and \(f^{\prime}(0)<0\).

  9. Let \(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}\) be the roots of the equation \(x^{n}-kx+1=0\) where \(n\geq 3\). Find the value of \(\sum_{i=1}^{n} \alpha_{i}^{n}\) in terms of \(k\) and \(n\).

  10. Let \(a,b,c\) be positive real numbers satisfying: \[ a+b+c = 10 \text{ and } ab+bc+ca=25 \] What is the maximum possible value of \(\text{min}(ab,bc,ac)\).

Part B: Subjective questions

Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1. The sides of a triangle are in arithmetic progression (A.P.) . The altitudes of the triangle are also in A.P. Prove that the triangle must be equilateral.

B2. A plane is partitioned into regions by three sets of parallel lines. There is no point that is common to three distinct lines. The number of lines in the first, second and third sets are \(x,y\) and \(z\), respectively.

  1. Find the number of regions formed by the lines in terms of \(x, y\) and \(z\). [5 marks]
  2. What is the minimum value of \(x+y+z\) for which it is possible to get at least 200 regions? [5 marks]

B3. (a) Find two continous functions \(f: \mathbb{R}\rightarrow\mathbb{R}\) and \(g: \mathbb{R}\rightarrow\mathbb{R}\) such that:

  • \(f(x)\) is differentiable everywhere but \(g(x)\) is not.
  • \(f(x)\times g(x)\) is differentiable everywhere.   [3 marks]

(b) Suppose \(f: \mathbb{R} \rightarrow \mathbb{R}\) is a differentiable map satisfying \(f(0)=0\) and \(f(1)=1\). For all real \(x\), we have \(\left|f^{\prime}(x)\right| \leq 2\).
What is the maximum possible value of \(\int_{0}^{1} f(x) d x\), over all such possible functions \(f\)?    [7 marks]

B4. Let \(m\) be a positive integer, such that \[ \frac{m+1}{m}=\frac{p+1}{p} \cdot \frac{q+1}{q} \] where \(p\) and \(q\) are positive integers exceeding \(m\).

  1. Prove that \((p-m)(q-m)=m(m+1)\).   [2 marks]
  2. Suppose \(\Phi(m)\) and \(\Phi(m+1)\), denote the number of positive divisors of \(m\) and \(m+1\), respectively. Count the number of positive integer pairs \( (p,q) \) that satisfy the above equation and express this number in terms of \(\Phi(m)\) and \(\Phi(m+1)\).   [6 marks]
  3. Using the result in the previous part, find the number of ways in which \(\frac{27}{26}\) can be expressed as a product of two rational numbers \(\frac{p+1}{p}\) and \(\frac{q+1}{q}\).  [2 marks]

B5.. We have natural numbers \(a,b\) and \(c\) such that: \[ a+b = \frac{ab}{c} \;\text{ and } \text{gcd}(a,b,c)=1 \] Prove that \(a+b\) is a perfect square.

B6. Prove that any real number \(\alpha\geq \frac{3\sqrt{3}}{2}\) can be expressed in the form: \[ \alpha=\sum_{n=0}^{\infty} \frac{a_{n+1}}{a_{n}^{3}} \] where \(a_{0}, a_{1}, a_{2}, \ldots\) is an increasing sequence of real numbers with \(a_{0}=1\).