MT #7: Combinatorics & Geometry
Timings: 17:00-20:00 Hrs Date: 6 May 2021
Part A: Short-answer type questions
Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg.
For this part, answers must be written without any explanation.
- We have 9 identical white beads and 2 identical black beads. How many distinct bracelets can we make using all the beads? Two bracelets are considered the same upto flipping and rotation.
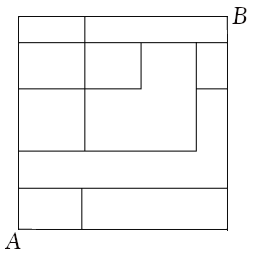
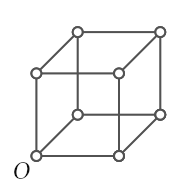
- We want to go from corner A to corner B in the figure shown below. If we can only move right or up, how many distinct ways are there to go from A to B?
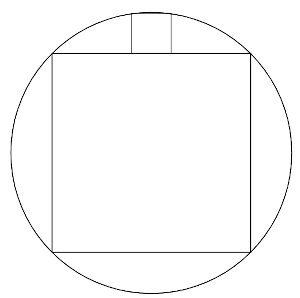
A unit square is inscribed in a circle. A smaller square sits on the top edge of the larger square. The top corners of the smaller square touch the circle. Find the length of the smaller square.
Count the number of ordered sequences of \(1\)s and \(5\)s that add up to \(13\).
For example, \( (1,1,5,1,5) \) and \( (1,1,1,1,1,1,1,1,1,1,1,1,1) \) are valid sequences.- Find the number of non-zero solutions to the equation: \(z^{2}+2 \bar{z}=0\).
- We have a triangle \(ABC\) and \(AD\) bisects the angle \(BAC\). We know the following measurements: \(AB=10\) cm, \(CD=2 BD\) and the area of the triangle \(ABC\) is 50 sq. cm. Find the value of the \(\angle BAD\) in degrees.
- In the complex plane shown below, \(PQR\) is an arc with center at \(A\). The values of the points are: \(A=-1+0i\), \(P=-1+\sqrt{2}+\sqrt{2}i\), \(Q=1+0i\) and \(R=-1+\sqrt{2}-\sqrt{2}i\). Which pair of inequalities represents the the shaded region?
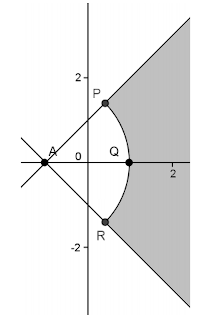
- \(|z+1|<2,|\arg (z+1)|<\frac{\pi}{2}\)
- \(|z-1|<2,|\arg (z-1)|<\frac{\pi}{2}\)
- \(|z+1|>2,|\arg (z+1)|<\frac{\pi}{4}\)
- \(|z-1|>2,|\arg (z+1)|<\frac{\pi}{4}\)
- Let \(t \in \mathbb{N}\). The number of elements in the set \(\left\{\left(\cos \frac{n\pi}{t}+i \sin \frac{n\pi}{t}\right) \mid n \in \mathbb{N}\right\}\) is
- Infinite
- \(t\)
- \(t+1\)
- \(2t\)
- \(2t+1\)
- \(2t-1\)
- None of the above.
An ant is initially at a corner of a cube. At each time step, it moves along an edge to a random adjacent vertex. What is the probability that it returns to the starting position after four time steps?
\(ABCD\) is a square such that the side \(AB\) lies on the line \(y=x+4\) and the points \(C\) and \(D\) lie on the parabola \(y^2 = x \). Find a possible set of values for the points \(A,B,C\) and \(D\).
Part B: Subjective questions
Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.
Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.
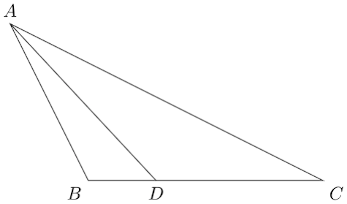
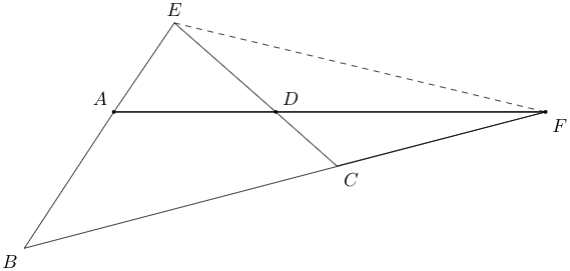
B1. \(ABCD\) is a cyclic quadrilateral with side lengths as follows. \(AB = 6\) cm, \(BC = 12\) cm, \(CD = 3\) cm and \(DA = 6\) cm. Find the length of \(EF\) in the figure shown below.
B2. Count the number of ordered pairs of positive integers \( (a, b) \) such that the complex number \(z=a+bi\) satisfies \(|z+2|^{2}+|z-2|^{2}<40\).
B3. Let \([n]\) denote the set of numbers \( \{1,2,\ldots,n\} \). A bijection \(f:[n] \rightarrow [n]\) is said to be neat if for every \(i \in \{2,3,\ldots,n\}\) we can find a \(j< i\) such that \( |f(i)-f(j)| = 1 \).
(a) Prove that if \(f\) is neat bijection, then either \(f(n)=1\) or \(f(n)=n\). [4 marks]
(b) Find the number of neat bijections. [6 marks]
B4. For any given \(k\), show that the following equation has a solution where \(x_i\geq 3\) for all \(i\) and \(y\geq 3\). \[ x_{1} !x_{2} ! \cdots x_{k} !=y ! \]
B5. Let \( A=(0,0) \) and \( C=(1,0) \). Let \(B\) be a point on the line \(y=x+1\). Suppose \(B\) is the point of tangency of a circle with chord \(AC\). In other words, a circle with chord \(AC\) touches the line \(y=x+1\) at point \(B\).
(a) Find all possible values of point \(B\). [5 marks]
(b) Among the possible values found in (a), for which value is the angle \(ABC\) maximized? Explain. [5 marks]
B6. Let \(A\) be a sequence of \(n\) positive integers. Let us note down the sum of every contiguous sub-sequence of \(A\) into a set \(S\). The sequence \(A\) is called k-good if \(S\) contains all the values in the range \( \{1..k\}\).
For example, A=[1,2,3] has the following subsequences: [1],[2],[3],[1,2],[2,3] and [1,2,3]. The sums of the subsequences are 1, 2, 3, 3, 5 & 6 respectively. Hence, [1,2,3] is 3-good but not 4-good.
The sequence \([1, 3, 2]\) is 6-good. The contiguous subsequences that give numbers upto 6 are:\( [1],[2],[3],[1,3],[3,2]\) and \([1,2,3]\).
Find a sequence \(A\) of length 20 that is 100-good.