Link Search Menu Expand Document
CMI Entrance Exam

MT #6: Full-syllabus

Timings: 17:00-20:00 Hrs    Date: 1 April 2021

Part A: Short-answer type questions

Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg.

For this part, answers must be written without any explanation.

  1. Find a non-constant polynomial that divides all the polynomials in the set: \[ \mathcal{P} = \{ P_k: P_k(x) = x^{3k+2}+x+1, k\in \mathbb{N} \} \]
  2. Let \(\alpha_1,\ldots,\alpha_n\) denote the \(n\) roots of unity. Let \(\alpha_1=1\). What is the value of the following product? \[ \prod_{i=2}^n (1-\alpha_i) \]
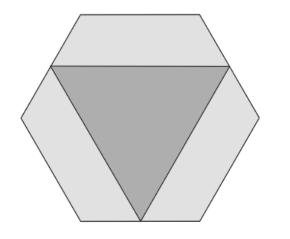
  3. We have a regular hexagon whose area is 1 sq.unit. A triangle is formed by joining the midpoints of alternate sides as shown below. What is the area of the triangle?

  4. Let \( \displaystyle f(x) = \frac{x^2e^{x^2}}{1-x^2} \). Find the \(6\)th derivative of \(f\) evaluated at 0, that is, \(f^6(0)\).
  5. The number of real valued solutions to the equation \(e^x=\sin x\) is:
    1. 0
    2. 1
    3. 2
    4. 4
    5. none of the above.
  6. Find a line \(l\) that intersects the four lines given below. The lines are in \(\mathbb{R}^3\). Express the equation of \(l\) in the parameterized form as given for \(l_i\)s.
    \begin{align*} l_1: &\; (1,0,0) + t(0,0,1) \\ l_2: &\; (0,1,0) + t(1,0,0) \\ l_3: &\; (0,0,1) + t(0,1,0) \\ l_4: &\; (0,0,0) + t(6,6,-1) \end{align*}
  7. Suppose \(a_i\) and \(b_i\) are real numbers such that \(\sum_1^\infty a_i^2\) and \(\sum_1^\infty b_i^2\) converge. Which of these statements is true?
    1. The sequence \(\sum_1^\infty |a_i-b_i| \) converges.
    2. The sequence \(\sum_1^\infty |a_i-b_i|^{3/2} \) converges.
    3. The sequence \(\sum_1^\infty (a_i-b_i)^2 \) converges.
    4. The sequence \(\sum_1^\infty (a_i-b_i)^3 \) converges.

  8. Let \(\phi(n)\) denote the number of positive integers less than \(n\) that are relatively prime to \(n\). In other words, \(\phi(n)\) counts all \(m\) such that \(\operatorname{gcd}(m, n)=1\).

    The number \(n=220358\) is a product of three primes \(p\), \(q\) and \(r\). We also know that \(\phi(n) = 109480.\)

    Find the values of \(p\), \(q\) and \(r\).

  9. Calculate the determinant of the matrix given below: \begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 2 & 3 & 4 & 5 & 6\\ 3 & 3 & 3 & 4 & 5 & 6\\ 4 & 4 & 4 & 4 & 5 & 6\\ 5 & 5 & 5 & 5 & 5 & 6\\ 6 & 6 & 6 & 6 & 6 & 6\\ \end{bmatrix}

  10. Suppose \( S=\{1,2,3,4,5,6,7\} \). Find the number of pairs \( (A,B) \) that can be formed such that \(A \subseteq S\) and \(B\subset A\).

Part B: Subjective questions

Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1. Let \( p(x)=a_{0}+a_{1} x+a_{2} x^{2}+a_{3} x^{3}\) be a polynomial with integer coefficients such that \(a_{0}\) and \(a_{3}\) are odd numbers.

  1. Suppose \(p\) has a rational root \(\frac{p}{q}\), where \(\text{gcd}(p,q)=1\). Prove that both \(p\) and \(q\) must be odd.
  2. Suppose \(a_0,a_3\) and \(a_0+a_1+a_2+a_3\) are all odd. Prove that \(f\) has no rational roots.

B2. By induction or otherwise, show that: \[ \binom{n}{2} ! >\; 2^{n^2} \] for all \(n\geq 6\).

B3. We are given two positive integers \(a>2\) and \(n\) such that the following \(n+1\) numbers are all composite numbers: \[ a,a+1,a+2,\ldots,a+n \] Prove that there exists an integer \(t>1\) such that the following consecutive numbers are all composite: \[ a^t,a^t+1,a^t+2,\ldots,a^t+n \]

B4. Consider the trapezoid \(ABCD\) in which \(|AD|=|BC|\). Prove that the centroid of the triangle \(ABD\) lies on the line \(CF\). Here, point \(F\) is the projection of \(D\) on \(AB\).

B5. Let \(\pi\) denote a permutation of numbers from \(1\) to \(12\). We denote the number at the \(i\)th position by \(\pi(i)\). For example, if the permutation is \([1,12,11,2,3,4,5,6,7,8,9,10]\), then \(\pi(1) = 1\), \(\pi(2)=12\), \(\pi(3)=11\), etc. Count the number of permutations \(\pi\) that satisfy the following condition: \[ \pi(i) < \pi(i+1) \;\;\text{for } i \in \{1,2,4,5,7,8,9,11\} \] Write your answer as a single number (without any factorials or binomials).

B6. We have a function \(f:\mathbb{R}\rightarrow\mathbb{R}\) that is twice differentiable and satisfies the following equation: \[ \int_{x-y}^{x+y} f(t) dt = 2yf(x) \] Prove that \(f(x)=ax+b\) for some \(a,b\in\mathbb{R}\).