MT #5: Integral Calculus

Timings: 10:30-13:30 Hrs    Date: 21 March 2021

Part A: Short-answer type questions

Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg.

For this part, answers must be written without any explanation.

1. Suppose \(n\) is a fixed positive integer. If \( \int_{1}^{k} x^{n-1} dx = \frac{1}{n} \), what is the value of \(k\)?
2. Evaluate \( \displaystyle \int_{0}^{2} \frac{1}{\left( x-\frac{1}{2} \right)^2+\frac{3}{4}} dx \).
3. Let \( f(x) \) be a continuous real-valued function on \([0, 1]\) for which \[ \int_{0}^{1} f(x)dx = 0 \text{ and }\;\;\; \int_{0}^{1} xf(x) dx = 1 \] Give an example of such a function.
4. Consider the integral \( \int_{0}^{\infty} \frac{ \sin^2 x }{\pi^2 - x^2} dx \). Which of these statements are true?
   (a) The integral does not exist as the function is not defined at \( x=\pi \).
   (b) There is a removable singularity at \(x=\pi\) but the integral does not exist.
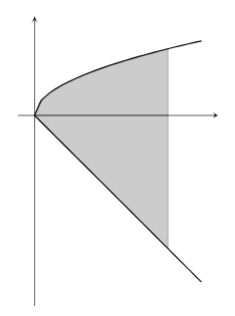
   (c) There is a removable singularity at \(x=\pi\) and the integral exists.
5. Find the volume of the solid obtained when the region bounded by \( y=\sqrt{2x}\), \( y=-x \) and the line \(x=6\) is revolved around the x-axis.
   

   

6. Let \( f(x) = \sum_{n=0}^{\infty} \frac{x2^n}{n!} \) be a function defined in the interval \( [0,10] \). Find the value of: \[ \int_{0}^{10} f(x) dx \]
7. For any real number \(x\), let \([x]\) denote the greatest integer \(m\) such that \(m \leq x\). Find the value of \( \int_{-2}^{2} [x^2 – 2]dx \).
8. What is the area bounded by the curve \( y = \ln x \), the x-axis and the straight line \(x=3\)?
9. Suppose \(f(x)\) is a double differentiable function with \(f^{\prime}(0) = 1\) and \(f^{\prime}(1) = 2\). What is the value of the integral below? If it possible for the integral to take multiple values, write Indeterminate. \[ \int_{0}^{1} f^\prime(x) f^{\prime\prime}(x) dx \]
10. Compute the limit: \[ \lim_{n\rightarrow\infty} n^3 \int_{0}^{1/n} x^{100x+2} dx \]

Part B: Subjective questions

Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1. Let \( f:[0,1] \rightarrow \mathbb{R}^+ \) be a continous function such that \( \int_{0}^{1} f(t) dt = \frac{1}{3} \). Show that there exists \( c\in(0,1) \) such that \( \int_{0}^{c} f(t) dt = c-\frac{1}{2}\).

B2. Let \( f(x) \) be a real-valued function defined on the interval \( [1,\infty) \). The following equations hold: \begin{align*} f(1) &= 1 \\ f^{\prime}(x) &= \frac{1}{x^2+f(x)^2} \end{align*}

Prove that \( \lim_{x\rightarrow \infty} f(x) < 1 + \pi/4 \).

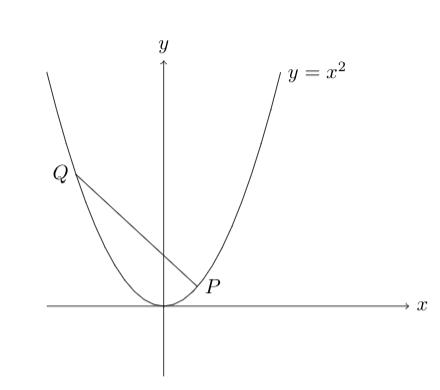
B3. Consider the parabola given by \(y = x^2\). The normal is constructed at a point \(P\) and meets the parabola again in \(Q\). Determine the coordinate of \(P\) for which the arc length along the parabola between \(P\) and \(Q\) is minimized.

B4. Let \( f(x) \) be a continous function defined on the interval \(I=[0,1]\) with the property \[ yf(x) + xf(y) \leq 1 \] for \(x,y\) in \(I\).
(a) Prove that: \[ \int_{0}^{1} f(x) dx \leq \frac{\pi}{4} \] (b) Find a function \( f(x) \) for which equality holds in problem (a).

B5. Suppose \(\displaystyle I_{n}= \int_{0}^{2} (2x-x^2)^{n}dx\). Prove that \(\displaystyle \lim_{n\rightarrow \infty} I_{n} = 0 \).

B6. Let \( \displaystyle f(x) = \frac{x}{1+x^5\sin^2x} \). Prove that \(\displaystyle \int_0^\infty f(x)\; dx\) is bounded.