Mock test #2 ‘22: Full-syllabus test
Timings: 14:00-17:00 Hrs Date: 18 March 2022
Instructions
- You are responsible for keeping time. Email all your solutions by 17:05 Hrs IST.
- Write your answers with a dark pen on white paper.
- Find an email from me with the subject line ‘CMI Tomato: Second mock test of 2022’. Send your solutions (images) as replies to this email.
- Adjust/Reduce the resolution of the camera so that each image is less than 500 KB in size.
- As per the rules of CMI entrance exam, a simple calculator may be used.
- Total marks: 100 (10x4=40 for Part A + 6x10=60 for Part B)
For students who miss the live test
Self-administer the mock test and email your solutions before 19 March, 23:59 Hrs IST. Your solutions will be evaluated but marks won’t be counted for official use in the future. Solutions submitted after 19 March, 23:59 Hrs will not be evaluated.
Part A: Short-answer type questions
Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg or PartA.png.
For this part, answers must be written without any explanation.
Which of the following statements is true?
(a) If a polygon inscribed in a circle has equal sides then it has equal angles.
(b) If a polygon inscribed in a circle has equal angles then it has equal sides.
(c) If a polygon has an inscribed circle, i.e. all its sides are tangent to the circle, and its sides are equal, then its angles are also equal.If \(S=\{a, b, c\}\) and the relation \(R\) on the set \(S\) is given by \(R=\{(a, b),(c, c)\}\), then \(R\) is
(a) reflexive and transitive
(b) reflexive but not transitive
(c) not reflexive but transitive
(d) neither reflexive nor transitive.If \(a+b+c=0\), then the quadratic equation \(3 a x^{2}+2 b x+c=0\) has
(a) at least one root in \((0,1)\).
(b) one root in \((1,2)\) and other in \((-1,0)\).
(c) both imaginary roots.
(d) a repeated rootLet \( \left[a\right] \) denote the largest integer smaller than or equal to \(a\). Then, \(\lim_{x \rightarrow 0} x\left[\frac{1}{x}\right]\) is
(a) 0
(b) 1
(c)-1
(d) does not exist.If \(\alpha\) and \(\beta\) are the roots of \(x^{2}+3 x+1\), find the value of \(\left(\frac{\alpha}{\beta+1}\right)^{2}+\left(\frac{\beta}{\alpha+1}\right)^{2}\).
Let \(f(x)\) be the function defined on \(\mathbb{R}\) such that \(f(x)=x\), for all \(x \leq 1\) and \(f(x)=\) \(a x^{2}+b x+c\), for \(x>1\). The triples \((a, b, c)\) such that \(f(x)\) is differentiable at all real \(x\) are of the form:
(a) \((a, 1-2 a, a)\)
(b) \((1,0,0)\) only
(c) \((a,-2 a, a)\)
(d) \((0,1,-1)\) onlyThe system of equations \[ \begin{align*} 2x+py+6z&=8 \\ x+2y+qz&=5 \\ x+y+3z&=4 \end{align*} \] has no solution for
(a) \(p \neq 2, q \neq 3\)
(b) \(p \neq 2, q=3\)
(c) \(p=2, q=3\)
(d) \(p=2, q \neq 3\)Suppose \(f\) is continuous in \([0,2]\) and differentiable in \((0,2)\). If \(f(0)=0\) and \(\left|f^{\prime}(x)\right| \leq 1 / 2\) for all \(x \in[0,2]\), then
(a) \(|f(x)| \leq 1\).
(b) \(|f(x)| \leq 1 / 2\).
(c) \(f(x)=2 x\).
(d) \(f(x)=3\) for at least one \(x \in[0,2]\).Let \(f\) be a differentiable real valued function on \((-1,4)\) such that \(f(3)=6\) and \(f^{\prime}(x) \geq-1\) for all \(x\). What is the the largest possible value of \(f(0)\)?
There are 18 ways in which \(n\) identical balls can be grouped such that each group contains equal number of balls. Then the minimum value of \(n\) is
(a) 120
(b) 180
(c) 160
(d) 90
Part B: Subjective questions
Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.
Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.
B1. A regional math competition saw a participation from 200 students. The paper had 6 problems. We know that each problem was correctly solved by at least 120 students. Prove that there must be two students such that every problem was solved by at least one of these two students.
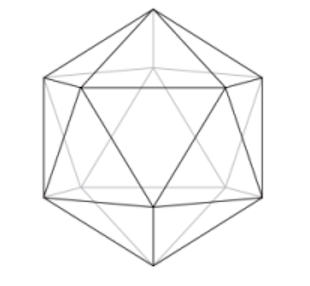
B2. An icosahedron is a regular polyhedron with 20 identical equilateral triangle faces. See the picture below. Each side of the icosahedron is 1 cm in length. What is the length of the longest line segment that can be contained inside an icosahedron?
B3. Prove the following inequality for all integers \(a,b\geq 2\): \[ \frac{1}{\operatorname{gcd}(a, b-1)}+\frac{1}{\operatorname{gcd}(a-1, b)} \geq \frac{2}{\sqrt{a+b-1}} \]
B4. (a) In \(\triangle A B C\), the altitude to \(\overline{A B}\) from \(C\) partitions \(\triangle A B C\) into two smaller triangles, each of which is similar to \(\triangle A B C\). If the side lengths of \(\triangle A B C\) and of both smaller triangles are all integers, find the smallest possible value of \(A B\).
B4. (b) In quadrilateral \(A B C D\), diagonals \(A C\) and \(B D\) intersect at \(E\). If \(A B=B E=5, E C=C D=7\), and \(B C=11\), compute \(A E\).
B5. Prove that among any six consecutive positive integers, we can always find a number that is relatively prime to the other five numbers.
B6. Show that the following integral converges: \[ \lim_{B \rightarrow \infty} \int_{0}^{B} \frac{\cos (x)}{2x} \cos \left(x^{2}\right) dx \]