Mock test #1 ‘22: Full-syllabus test

Timings: 14:00-17:00 Hrs    Date: 4 March 2022

Instructions

• You are responsible for keeping time. Email all your solutions by 17:05 Hrs IST.
• Write your answers with a dark pen on white paper.
• Find an email from me with the subject line ‘CMI Tomato: First mock test of 2022’. Send your solutions (images) as replies to this email.
• Adjust/Reduce the resolution of the camera so that each image is less than 500 KB in size.
• As per the rules of CMI entrance exam, a simple calculator may be used.
• Total marks: 100 (10x4=40 for Part A + 6x10=60 for Part B)

For students who miss the live test
Self-administer the mock test and email your solutions before 5 March, 23:59 Hrs IST. Your solutions will be evaluated but marks won’t be counted for official use in the future. Solutions submitted after 5 March, 23:59 Hrs will not be evaluated.

Part A: Short-answer type questions

Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg or PartA.png.

For this part, answers must be written without any explanation.

1. The values of \(k\) for which the line \(y=k x\) intersects the parabola \(y=(x-1)^{2}\) are

   (a) \(k \geq-4\).
   (b) \(k \leq 0 \).
   (c) \(-4 \leq k \leq 0\).
   (d) \(k \geq 0\) or \(k \leq-4\).
   

2. Let \(\operatorname{gcd}(a, b)=1\), then \(\operatorname{gcd}\left(a+b, a^{2}-a b+b^{2}\right)=\)
   (a) 2
   (b) 1 or 2
   (c) 1 or 3
   (d) 2 or 3
   

3. Find the remainder when \(\displaystyle \sum_{r=1}^{50} r! \) is divided by 12.

4. Find the number of solutions to the equation \(\sqrt{1-\sin x}=\cos x\) in the interval \([0,5 \pi]\).

5. The number of real roots of the equation \(x^6-x+1\) is:

   (a) Zero.
   (b) exactly 1.
   (c) exactly 2.
   (d) exactly 4.
   

6. Alice has the five letters: A, B, C, D, E. How many ways can she rearrange the letters into three words? The order of the words matter. For example, "AB C DE" and "C AB DE" are different rearrangements.

7. Find the sum of the coefficients of the polynomial obtained after expanding and collecting the terms of the product \(\left(5x^{2}-5x+1\right)^{10}\left(x^{4}-2x+1\right)^{20}\).

8. Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be a continuous function such that \(|f(x)-f(y)| \geq|x-y|\) for all real numbers \(x, y\). Then which of the options below are true?
   (a) \(f\) is one-one
   (b) \(f\) is onto
   (c) \(f^{-1}\) may not exist
   (d) \(f^{-1}\) is continuous
   

9. Let \(\left\{a_{n}\right\}\) and \(\left\{b_{n}\right\}\) be two sequences of non-zero real numbers. We say that \(\left\{a_{n}\right\}\) and \(\left\{b_{n}\right\}\) are mostly equal if \(\lim_{n \rightarrow \infty} \frac{a_{n}}{b_{n}}=1\). Which of the following sequences are mostly equal?
   (a) \(a_{n}=n-2\sqrt{n}, b_{n}=n\).
   (b) \(a_{n}=n^{2}+\sqrt[3]{n}, b_{n}=n\).
   (c) \(a_{n}=n!, b_{n}=n^{n}\).
   (d) \(a_{n}=\left(1+\frac{1}{n}\right)^{n}, b_{n}=e\).
   
   

10. We have two identical cups denoted by M and W. Cup M contains a milk and cup W has equal amount of water in it. One spoon of milk is transferred to cup W and then one spoon of the mixture in cup W is transferred to cup M. Then which of the following is true?
    (a) The amount of milk in cup W bigger than the amount of water in cup M.
    (b) The amount of milk in cup W smaller than the amount of water in cup M.
    (c) The amount of milk in cup W is equal to the amount of water in cup M.
    (d) Can't say since it depends on the size of the spoon.
    

Part B: Subjective questions

Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1 (a) Find a four digit number which on division by 149 leaves a remainder of 17 and on division by 148 leaves a remainder of 29 .

B1 (b) Find all the primes \(p\) such that \(2^p+p^2\) is also prime.

B2. Three points \(A, B\) and \(C\) lie inside a circle whose radius is 1 cm. Show that \(B C^{2}+C A^{2}+A B^{2}\) is less than or equal to 9 sq. cm.

B3. We have three colors: red, blue and green. In how many ways can we color the vertices of an octagon such that no two adjacent vertices have the same color? A valid coloring of the octagon is shown below. Adjacent vertices are connected by a line segment.

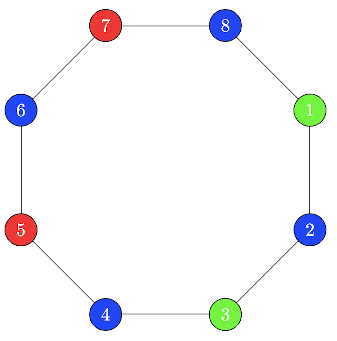
Remark. If we were coloring a triangle instead of an octagon, there would be 6 ways to do it. The first vertex can be colored in 3 ways, the second vertex can be colored 2 ways and the color of the third vertex would be fixed.

B4 (a). Simplify \( \sqrt[3]{2+\sqrt{5}} + \sqrt[3]{2-\sqrt{5}}\).

B4 (b). Which is larger: \(\sqrt[8]{8!}\) or \( \sqrt[9]{9!} \)?

B5.

1. Suppose \(f\) is a differentiable function from the \(\mathbb{R}\) into \(\mathbb{R}\). Suppose \(f'(x) > f(x)\) for all \(x \in \mathbb{R}\) , and \(f(x_0) = 0\) for some \(x_0 \in \mathbb{R}\). Prove that \(f(x) > 0\) for all \(x > x_0\) .
2. Show that the equation \(Ae^x = 1 + x + \frac{x^2}{2}\) , where \(A\) is a positive constant, has exactly one real root.

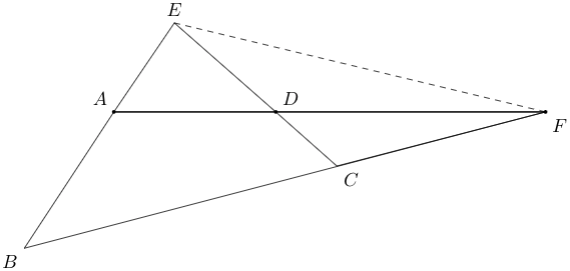
B6. \(ABCD\) is a cyclic quadrilateral with side lengths as follows. \(AB = 6\) cm, \(BC = 12\) cm, \(CD = 3\) cm and \(DA = 6\) cm. Find the length of \(EF\) in the figure shown below.