Functions
One-to-one function
A1, 2013
For sets \(S\) and \(T,\) let \(f: S \rightarrow T\) and \(g: T \rightarrow S\) be functions such that \(f(g(x))=x\) for each \(x \). State which of the statements are true.
- (a) The function \(f\) must be one-to-one.
- (b) The function \(g\) must be one-to-one.
- (c) The function \(f\) must be onto.
- (d) The function \(g\) must be onto.
Solution
False-True-True-False.
If \(g\left(x_{1}\right)=g\left(x_{2}\right),\) then \(x_{1}=f\left(g\left(x_{1}\right)\right)=f\left(g\left(x_{2}\right)\right)=x_{2},\) so \(g\) is one-to-one. Also \(f\) is onto because each \(x \in T\) is in the image of \(f,\) namely \(x=f(g(x)) .\) The other two statements are false, for example by constructing an \(S\) that is a larger finite set than \(T\).
Composition
B1a, 2021
\(f\) is a function defined on the domain \(S\) and codomain \(T\) and \(g\) is a function defined on the domain \(T\) and codomain \(U\). Fill in the blanks with with one of the four options.
If \(g\circ f\) is one-one then, \(f\) is \(\underline{.......}\) and \(g\) is \(\underline{......}\).
If \(g\circ f\) is onto then, \(f\) is \(\underline{.......}\) and \(g\) is \(\underline{......}\).
Options:
A: One-one and onto.
B: One-one but need not to be onto.
C: Onto but need not to be one-one.
D: Need not to be one-one and need not be onto.
Solution
Ans. B-D-D-C.
Explanation. If \(g\circ f\) is one-one, the \(f\) must be one-one. If not, there are two elements \(x\) and \(y\) with \(x\neq y\) such that \( f(x) = f(y) \), which implies that \(g(x) = g(y)\). A contradiction. However, \(f\) need not be onto and \(g\) need not be onto or one-one as the example below shows.
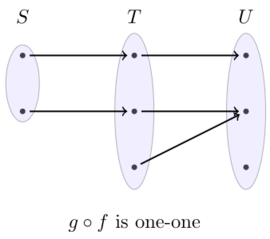
If \(g\circ f\) is onto, then \(g\) must be onto since every element in \(U\) must be reached by some element from \(S\) via \(T\). As the example below shows, this the only constraint.
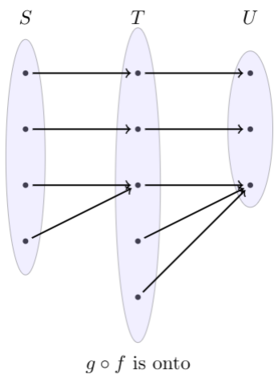
Asymptotes
A5, 2020
Write whether the \(3\) functions \(\frac{x^3}{(x^2-x)}, \ \frac{(x^2-x)}{x^3},\ \frac{(x^3-x)}{(x^3+x)}\) have horizontal asymptotes, vertical asymptotes and removable discontinuities.
Solution
How to find a horizontal asymptote?
Let us consider the case when the given function is of the form: \[ f(x) = \frac{a_1x^m+a_2x^{m-1}+\cdots+a_m}{b_1x^n+b_2x^{n-1}+\cdots+b_n} \]- If \(m> n\), then there is no horizontal asymptote.
- If \(m< n\), then \(y=0\) a horizontal asymptote.
- If \(m=n\), then \(y=a_1/b_1\) a horizontal asymptote.
How to find a vertical asymptote?
Vertical asymptotes occur at those points where the denominator is zero and the numerator is non-zero.The first two functions have \(x=1\) and \(x=0\) as their vertical asymptotes. The denominator is always positive for the third function, so there are no vertical asymptotes for this function.
Removable discontinuities
In all the functions, the term \(x\) can be factored out from the numerator and the denominator. Hence, \(x=0\) is a removable discontinuity for all the functions.
Constrained function
B4, 2020
i) A continuous function \(f(x)\) has the property that \(f(x^2)=f(x)^2.\) If the domain of \(f\) is \([0,1]\) and \(f(0)\neq 0,\) then show that \(f\) is unique and find \(f.\)
Solution
Since \(f(0)\) is non-zero, \(f(0)=f(0)^2 \implies f(0)=1\). Since \(f(x) = f(\sqrt{x})^2 \), the range of \(f\) is non-negative. We will show that \(f(x)=1\).
Let \(p\in (0,1)\) be an arbitrary point and \(f(p) = q\). \begin{align} f(p^2) &= f(p)^2 = q^2 \\ f(p^4) &= q^4 \\ &\vdots \\ f(p^{2^n}) &= q^{2^n} \end{align} Since \(|p|< 1\) the sequence \({p^{2^n}}\) converges to 0 as \(n\rightarrow \infty\). Since the function is continuous: \[ f(0) = 1 = \lim_{n\rightarrow \infty} q^{2^n} \] The sequence \(q^{2^n}\) must converge to 1. This is possible only if \(q=1\). By continuity, \(f(1)=1\) too. Therefore, the conditions imply that \(f\) is unique and that \(f(x)=1\).
ii) Consider the same property of \(f,\) but the domain of the function being \((0,\infty).\) Show that either \(f(x)=0\ \forall x\) or \(f(x)\neq 0\) \(\forall\) \(x.\)
Solution
The proof is similar to the previous proof. For \(x=1\) we have: \[f(1^2) = f(1)^2 \implies f(1)(f(1)-1) = 0\] So \(f(1)\) is either 0 or 1.
Lemma. If \(f(1)=0\), then \(f(x)=0\).
Proof. For a contradiction, let us say there exists a point \(p\) such that \(f(p)=q\), where \(q>0\). \begin{align} f(\sqrt{p})^2 &= f(p) = q \\ f(\sqrt{p}) &= \sqrt{q} \\ f(p^{ 1/2^n } ) &= q^{1/2^n} \\ \lim_{n\rightarrow \infty} f(p^{ 1/2^n } ) &= q^{1/2^n} \\ f(1) &= 1 \;\;\;\; \mbox{ (a contradiction) }\;\; \square \end{align}
Lemma. If \(f(1)=1\), then \(f(x) \neq 0 \;\forall x\).
Proof. For a contradiction, let us say there exists a point \(p\) such that \(f(p)=0\). \begin{align} f(\sqrt{p})^2 &= f(p) = 0 \\ f(\sqrt{p}) &= 0 \\ f(p^{ 1/2^n }) &= 0 \;\;\;\;\mbox{ (by induction)}\\ \lim_{n\rightarrow \infty} f(p^{ 1/2^n } ) &= 0 \\ f(1) &= 0 \;\;\;\; \mbox{ (a contradiction) }\;\; \square \end{align}
iii) Show that there exist infinitely many continuous functions \(f(x)\) with the same property and with domain \((0,\infty)\) such that \(\int_0^{\infty}f(x)dx<1.\)
Solution
For any \(p>4\), the following function satisfies the conditions: \[ f(x) = \left\{\begin{array}{lr} x& \text{for } 0 < x \leq 1\\ x^{-p} & \text{for } 1 < x < \infty \\ \end{array} \right. \]
\begin{align} \int_0^{\infty}f(x)dx &= \int_0^{1}x dx + \int_1^{\infty} x^{-p} dx \\\\ &= \left. \frac{x^2}{2} \right \rvert_{0}^{1} \; +\; \left. \frac{x^{-p+1}}{-p+1} \right \rvert_{1}^{\infty} \\\\ &= \frac{1}{2} + \frac{1}{p-1} \\\\ &< \frac{5}{6} \;\;\;\mbox{ since }\; p>4 \end{align}
Surjective if and only if injective
B11, 2011
A function \(f\) from a set \(X\) to itself satisfies \(f^{m}=f^{n}\) for fixed positive integers \(m\) and \(n\) with \(m> n\). The notation \(f^{n}\) stands for \(f \circ f \circ \cdots \circ f(n\) times). Show that \(f\) is one-to-one (injective) if and only if \(f\) is onto (surjective).
Solution
Claim 1: If \(f\) is one-to-one, then it is onto.
Proof: Let \(m=n+k\). \[f^m(x) = f^n(x) \implies f^n( f^k(x) ) = f^n(x) \implies f^k(x) = x \text{ for all } x\] The second implication follows since \(f(p)=f(q)\) implies that \(p=q\) for a one-to-one function. Since \(f^k\) is an identity function, its range must be \(X\). So the range of \(f\) must also be \(X\), which proves the claim. \(\;\square\)
Claim 2: If \(f\) is onto, then it is one-to-one.
Proof: We prove by contradiction. Assume that \(f\) is onto but not one-to-one. So there must be an \(x\) such that \(f(a_1) = f(b_1) = x\) for some \(a_1\neq b_1\). Since \(f\) is onto we should be able to find two numbers \(a_2\) and \(b_2\) such that \[ f(a_2) = a_1 \text{ and } f(b_2) = b_1 \] Also, \(a_1\neq b_1 \implies a_2\neq b_2\). It follows that: \[ f^2(a_2) = x \text{ and } f^2(b_2) = x \] In general, for every natural number \(t>1\), we should be able to find two different numbers \(a_t,b_t\) with the property that \(f^t(a_t) = f^t(b_t) = x\) and \(f(a_t) = a_{t-1} \text{ and } f(b_t) = b_{t-1} \). In particular, consider the numbers \(a_m\) and \(b_m\), where \(f^m(a_m) = f^m(b_m) = x\). Due to the condition \(f^m=f^n\), we have: \[ x = f^m(a_m) = f^n(a_m) = a_{m-n} = a_k \] \[ x = f^m(b_m) = f^n(b_m) = b_{m-n} = b_k \] This implies that \( a_k=b_k \), which is a contradiction.
Continuity of two functions
A10, 2017
Consider the following function: \[ f(x)=\left\{\begin{array}{ll} x^{2} \cos \left(\frac{1}{x}\right), & x \neq 0 \\ a & x=0 \end{array}\right. \]
(a) Find the value of \(a\) for which \(f\) is continuous.
(b) \(f^{\prime}(0)\)
(c) \(\lim_{x \rightarrow 0} f^{\prime}(x)\)
Solution
(a) \(\cos \left(\frac{1}{x}\right)\) is sandwiched between -1 and \(1,\) so \(\lim_{x \rightarrow 0} f(x)=0=a\) makes \(f\) continuous.
(b) Now \(f^{\prime}(0)=\lim_{h \rightarrow 0} \frac{h^{2} \cos \left(\frac{1}{h}\right)-0}{h}=\lim_{h \rightarrow 0} h \cos \left(\frac{1}{h}\right)\) which is similarly 0.
(c) For nonzero \(x,\) calculate \(f^{\prime}(x)=2 x \cos \left(\frac{1}{x}\right)+\sin \left(\frac{1}{x}\right),\) so \(\lim_{x \rightarrow 0} f^{\prime}(x)\) does not exist \(\operatorname{as} \lim_{x \rightarrow 0} 2 x \cos \left(\frac{1}{x}\right)=0\) and \(\lim_{x \rightarrow 0} \sin \left(\frac{1}{x}\right)\) does not exist.
