Link Search Menu Expand Document
CMI Entrance Exam

MT #1: Number theory & Trigonometry

Timings: 10:30-13:30 Hrs    Date: 7 Feb 2021

Part A: Short-answer type questions

Submission file: Write answers to all the ten questions on a single sheet of paper. Email a picture of your answer sheet. Name the file as PartA.jpg or PartA.png.

For this part, answers must be written without any explanation.

  1. If three numbers \(p\), \(p+2\) and \(p+4\) are primes. What is the value of \( p \)?

  2. List all the numbers between 1 and 1000 that are both divisible by 7 and have exactly six factors.

  3. Let \(x\) be a real number such that \( \sec x-\tan x=1/3 \). Evaluate \( \sec x+\tan x \).

  4. Consider the two numbers \(a\) and \(b\) whose prime factorizations are as follows: \[ a = 2\cdot 3\cdot 5^2 \cdot 7^3 \cdot 17^5 \cdot 23 \] \[ b = 2\cdot 3^2\cdot 5 \cdot 7^3 \cdot 11 \cdot 17 \]
    1. Write the prime factorization of the GCD of \(a\) and \(b\). [2 marks]
    2. Write the prime factorization of the LCM of \(a\) and \(b\). [2 marks]

  5. Imagine a rectangular carrom board \(ABCD\) with \(AB=17 \) cm and \(BC=16 \) cm. Assume the striker to be a point moving with no friction. The angle of reflection is equal to the angle of incidence. The striker is shot from point \(A\) at an angle \(\alpha\). It bounces off the edges twice and ends up at corner \(C\) as shown below. What is the value of \(\tan \alpha\)?

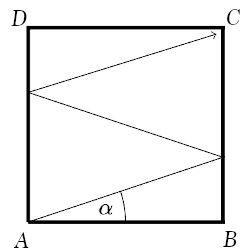
  6. How many ordered pair of integers \( (x,y) \) satisfy the equation \( \frac{x}{20} = \frac{20}{y} \)?

  7. Count the number of ordered pairs \( (a,b) \) that satisfy two conditions:
    • \(a\) and \(b\) are relatively prime positive integers
    • The product of \(a\) and \(b\) is \(10!\)

  8. Find the remainder when \(2021^{2021}\) is divided by 7.

  9. Identify the irrational numbers among the three numbers given below.

    1. \( \frac{2 \log (3)}{\log (2)+2 \log (3)} \)
    2. \( \frac{\log 14}{\log 18} \)
    3. \( \sqrt{3} + \sqrt{7} + \sqrt{17} - \sqrt{11}\)

  10. Consider the functions \(f_i\) given below:

    \begin{align} f_{1}=(\tan \theta)^{\tan \theta} & \;\; f_{2}=(\tan \theta)^{\cot \theta} \\ f_{3}=(\cot \theta)^{\tan \theta} & \;\; f_{4}=(\cot \theta)^{\cot \theta} \end{align}

    Identify the function whose value is greater than others in the domain \(\theta \in \left(0,\pi/4\right) \).

Part B: Subjective questions

Submission files: Each question in this part must be answered on a page of its own. Name the files as B1.jpg, B2.jpg, etc. In case you have multiple files for the same question, say B4, name the corresponding files as B4-1.jpg, B4-2.jpg, etc.

Clearly explain your entire reasoning. No credit will be given without reasoning. Partial solutions may get partial credit.

B1. Suppose \(x\) is an integer. What are the possible values of \( x^{65} \pmod{131} \) and why?

B2. Consider a coordinate grid made up of horizontal and vertical lines of the form \(x=k\) and \(y=k\), where \(k\in \mathbb{Z}\). Consider a line segment OA where O is the origin and A is the point \( (10,4) \). Notice that this line segment passes through the interior of 12 cells. In the figure below, the shaded cells are the ones through which the line passes.

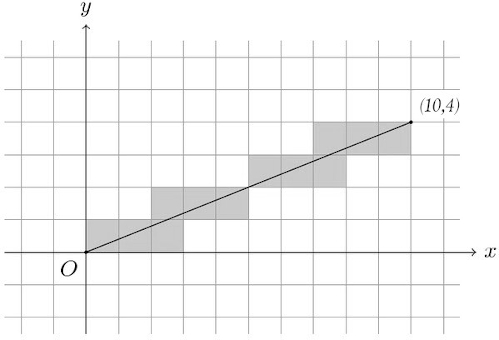
Suppose a line segment is drawn from the origin O to the point B at \( (48,54) \). How many cells would would OB pass through?

B3. Suppose \( f(x)=\cos^{-1}(\cos (\pi x)) \). Find the value of \( f(2.6) \).

B4. Find five unique positive integers \( b_{1}, b_{2}, \cdots, b_{5} \geq 2 \) such that: \[ \Large \frac{125}{76}=b_{1}-\frac{1}{b_{2}-\frac{1}{b_{3}- \frac{1}{b_4 - \frac{1}{b_5} } }} \]

You may find the following fact useful:

Let \(q\) and \(n\) be relatively prime positive integers such that \( 1 < q < n \). There exist unique integers \( k, r \) such that \( n=kq-r, 0 \leq r< q \).

B5. Find all the positive integer solutions to the following equation: \[ xyz-xy-yz-xz+x+y+z=52 \] Express the solutions as triplets \( (x,y,z) \).

B6. Prove that there are no integers \(x>0\) and \(n>1\) such that \( x(x+1) = 2442^n \).